Классическая математическая модель АД с кз ротором при частотном управлении в форме уравнений состояния
Для получения классической математической модели АД с кз ротором при частотном управлении в форме уравнений состояния используем четыре уравнения для цепей статора и ротора.
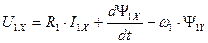 . (167)
. (167)
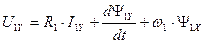 . (168)
. (168)
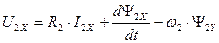 . (169)
. (169)
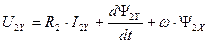 . (170)
. (170)
Из уравнений (167)-(170) можно получить четыре уравнения состояния математической модели АД с кз ротором при частотном управлении с учетом того, что 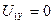 ,
, 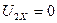 и
и 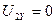 .
.
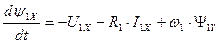 . (171)
. (171)
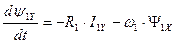 . (172)
. (172)
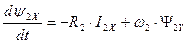 . (173)
. (173)
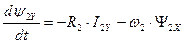 . (174)
. (174)
Структурная схема модели (см. рис. 17) в соответствии с уравнениями (171)-(174) должна содержать 4 интегратора для определения составляющих потокосцепления статора и ротора, 6 сумматоров и 5 умножителей и 5 пропорциональных звеньев. В четырех уравнениях (171)-(174) восемь неизвестных. Для уменьшения числа неизвестных воспользуемся уравнениями (175) и (176) и выразим 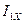 ,
, 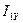 ,
, 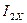 , и
, и 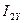 через
через 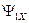 ,
, 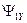 ,
, 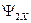 , и
, и 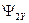 .
.
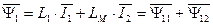 . (175)
. (175)
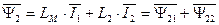 . (176)
. (176)
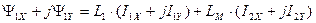 . (177)
. (177)
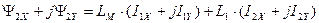 . (178)
. (178)
Преобразуем уравнения (177)-(178) и приравняем действительные и мнимые части в правой и левой частях уравнений ((177)-(178) и получим четыре уравнения для определения 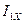 ,
, 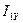 ,
, 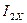 , и
, и 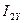 .
.
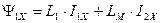 . (179)
. (179)
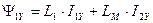 . (180)
. (180)
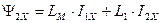 . (181)
. (181)
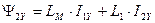 . (182)
. (182)
Решим уравнения (175) и (176). Получим
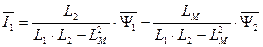 . (183)
. (183)
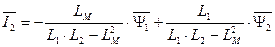 . (184)
. (184)
Представим комплексные векторы в выражениях (183) и (184) в алгебраической форме в виде вещественных и мнимых составляющих и преобразуем эти уравнения, приравнивая действительные и мнимые части в правой и левой частях выражений (185) и (186).
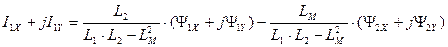 . (185)
. (185)
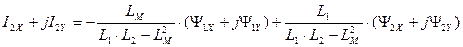 . (186)
. (186)
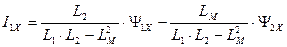 . (187)
. (187)
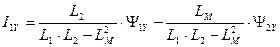 . (188)
. (188)
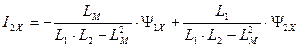 . (189)
. (189)
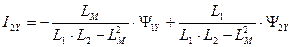 . (190)
. (190)
Для определения составляющих токов статора и ротора 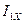 ,
, 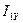 ,
, 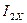 , и
, и 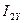 на структурной схеме необходимо дополнительно использовать 8 пропорциональных звеньев с коэффициентами передачи
на структурной схеме необходимо дополнительно использовать 8 пропорциональных звеньев с коэффициентами передачи 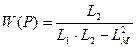 ,
, 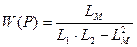 ,
, 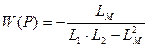 и
и 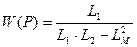 , подавая на их входы соответственно сигналы
, подавая на их входы соответственно сигналы 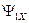 ,
, 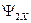 ,
, 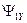 и
и 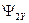 , а также 4 сумматора.
, а также 4 сумматора.

Рис. 17. Классическая математическая модель АД с кз ротором при частотном управлении в форме структурной схемы
Дата добавления: 2020-10-25; просмотров: 739;











