Обобщенные потокосцепления обмоток статора и ротора АД

Индуктивность 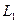соответствует полной индуктивности статорной обмотки, включающей ее индуктивность от потока рассеяния 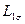, индуктивность от части основного магнитного потока, созданной самой обмоткой 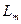, и индуктивность от части основного потока, созданной двумя другими обмотками статора, равная 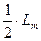. Индуктивность 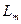рассчитывается при отсутствии токов в других обмотках статора. Таким образом, полная индуктивность обмотки статора от основного магнитного потока одной обмотки статора и магнитных потоков двух других обмоток статора, равная 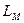, в 3/2 раза больше ее индуктивности 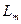, рассчитанной при отсутствии токов в других обмотках.

В силу симметрии статора, для других обмоток можно записать аналогичные выражения, а затем объединить фазные составляющие потокосцепления в обобщенный вектор потокосцепления статора при отсутствии токов ротора.

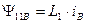. (35)

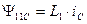. (36)

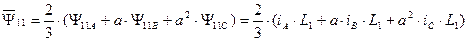- обобщенный вектор потокосцепления статора АД.

Наличие токов в обмотках ротора приведет к появлению дополнительных составляющих потокосцеплений обмоток статора. Если ось фазы «a» ротора смещена в пространстве на некоторый угол ( 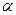), то взаимные индуктивности обмоток ротора и фазы «А» статора можно определить через соответствующие углы, образуемые их осями в виде – 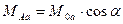, (37)

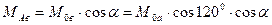, (38)

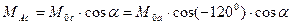, (39)

где 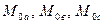– взаимные индуктивности при ( 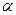) =0. Тогда «полное» потокосцепление обмотки фазы «А» статора при наличии токов ротора (т.е. потокосцепление обмотки статора в фазе «А» с магнитными потоками обмоток ротора) и с учетом того, что нулевой провод ротора отсутствует, будет равно

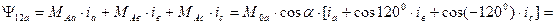
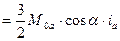. (40)

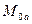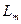Но взаимная индуктивность обмотки фазы А статора и обмотки фазы «а» ротора при нулевом смещении осей равна , т.к. параметры обмоток ротора приведены к статорным и приближенно можно считать, что при совпадении их осей картина магнитного поля будет такой же, как при совпадении осей статорных обмоток. Поэтому 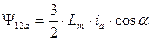. (41)

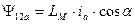. (42)

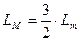. (43)

Аналогично можно получить для других потокосцеплений взаимной индуктивности обмоток фазы В и С статора и обмоток ротора.

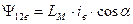. (44)

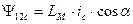. (45)

Объединяя уравнения (42), (44), (45), получим выражение для вектора обобщенного потокосцепления обмоток статора с магнитными потоками обмоток ротора.

.

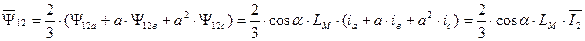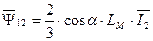. (46)

Объединяя потокосцепления фазных обмоток статора 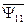(с потоками статора) и 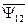(с потоками ротора) в обобщенный вектор потокосцепления, получим

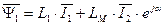. (47)

Аналогичное выражение, в силу симметрии связей между статором и ротором, можно записать для вектора обобщенного потокосцепления ротора.

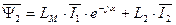. (48)

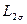- индуктивность рассеяния роторной обмотки;

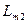- индуктивность основного потока роторной обмотки.

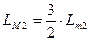- полная индуктивность фазной роторной обмотки с учетом магнитных потоков обмоток второй и третьей фаз.

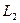- результирующая индуктивность фазной роторной обмотки с учетом магнитных потоков обмоток второй и третьей фаз и магнитного потока рассеяния роторной обмотки.

В выражениях (47) и (48) для потокосцеплени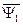й и 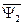векторы тока статора и ротора записаны в различных системах координат. Так в выражении для потокосцепления 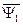ток статора записан в неподвижной системе координат « 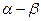», связанной со статором, а ток ротора во вращающейся системе координат « 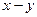», связанной с ротором (смещенной на текущий угол « 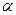» ). Полная запись выражений для потокосцеплени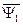й и 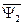с учетом индексов систем координат выглядит следующим образом.

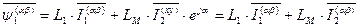. (49)

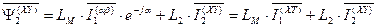. (49а)

В уравнениях (49) и (49а) имеют дело с переменными коэффициентами 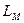, зависящими от взаимного расположения обмоток статора и ротора.