Особенности, свойства и преобразования «обобщенного» вектора и уравнений с «обобщенным» вектором

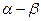Если вектор тока представлен в неподвижной системе координат « », то переход к новой системе координат « 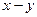», развернутой относительно исходной на некоторый угол 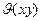осуществляется из соотношения аргументов комплексных чисел. Новая система координат «x-y» может вращаться с постоянной скоростью .

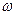Рис. 10. Вектор обобщенного тока в двух системах координат

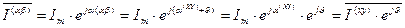. (50)

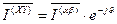. (51)

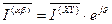. (52)

При этом следует заметить, что на угол 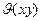не накладывается никаких ограничений, т.е. он может иметь постоянное значение, но 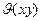может также изменяться произвольным образом. Обобщенный вектор можно представить также во вращающейся системе координат ( 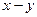). Для системы координат ( 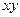), вращающейся с постоянной угловой частотой 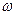угол 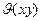равен .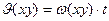

Преобразование координат можно осуществить не только от неподвижной системы к вращающейся, но и для двух систем координат, вращающихся с различными угловыми частотами.

Рис. 11. Вектор обобщенного тока в трех системах координат, две из которых вращаются

Пусть вектор 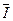представлен в системе координат « 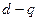», текущий угол которой относительно неподвижных координат составляет 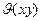. Тогда из соотношений углов преобразование координат можно записать в виде

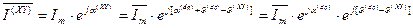. (53)

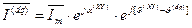. (54)