Составим на основе полученной математической модели ДПТ с НВ в форме уравнений состояния математическую модель ДПТ с НВ в форме структурной схемы.

Рис. 2. Структурная схема математической модели ДПТ с НВ

Для того, чтобы реализовать два уравнения состояния в форме структурной схемы, необходимо использовать два интегратора. На входе первого интегратора действует сигнал, равный 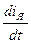, а на его выходе сигнал равен 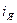. На входе второго интегратора действует сигнал, равный 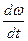, а на его выходе сигнал равен .

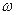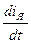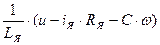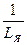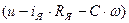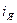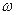В соответствии с уравнением (8) производная переменной состояния равна выражению . В этом математическом выражении величина постоянная, являющаяся параметром модели, а выражение в скобках включает координаты , и уравнения состояния (8). В соответствии с правилами теории автоматического управления (ТАУ) для реализации на структурной схеме выражения 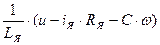необходимо на пропорциональное звено с передаточной функцией 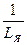подать сигнал, равный 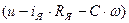. На выходе пропорционального звена (см. рис. 2) величина сигнала будет равна 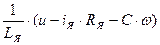. Для определения выражения 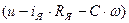на структурной схеме системы электропривода с ДПТ с НВ используется узел сравнения (вычитатель), выполняющий операцию вычитания сигналов 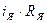и 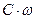из сигнала .

Реализация уравнения (9) в форме структурной схемы, соответствующей МЧ системы электропривода с ДПТ с НВ, рассмотрена в главе 7.