Математическая модель одномассовой механической части СЭП с постоянным моментом инерции

Проведем анализ основного уравнения движения электропривода.

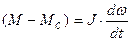(1)

где М – момент электрического двигателя (ЭД);

Мс – момент нагрузки;

J=const – приведенный к валу ЭД момент инерции электропривода (ЭП);

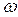- угловая скорость.

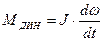(2)

Мдин - динамический момент.

Рассмотрим три варианта при анализе основного уравнения движения электропривода.

1.М = Мс; Мдин=0; .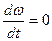

Если производная скорости равна нулю, то это означает, что

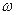=Const, т.е. имеет место равномерное движение механической части СЭП.

2. М>Мс; М дин>0;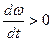

Если производная скорости больше нуля, то это означает, что 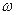увеличивается, т.е. имеет место ускоренное движение механической части СЭП.

3. М<Мс; М дин<0;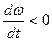

Если производная скорости меньше нуля, то это означает, что 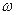уменьшается, т.е. имеет место заторможенное движение механической части СЭП.

Математическая модель одномассовой механической части СЭП с переменным моментом инерции

Основное уравнение движения электропривода для переменного момента инерции J=var.

,

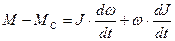где М – момент ЭД;

Мс – момент нагрузки;

J=var - момент инерции (переменный момент инерции);

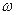- угловая скорость.