Адіабатичний процес

тобто газ здійснює роботу за рахунок спаду своєї внутрішньої енергії.

Запишемо це рівняння в диференціальному виді:

δА= - dU або PdV = -νC_v dT.(2.51)

Продиференціювавши рівняння стану ідеального газу отримаємо:

PdV+VdP=νRdT .(2.52)

Розділимо рівняння (2.52) на (2.51)

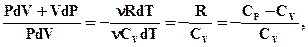
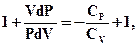чи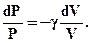

Інтегруючи цей вираз в межах від V₁ до V₂ відповідно від Р₁ до Р₂ і після потенціювання, отримаємо:

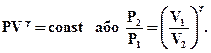(2.53)

Отриманий вираз є рівняння адіабатичного процесу. Ці рівняння називають рівнянням Пуассона.

На площині (Р, V) процес адіабатичного розширення (чи стискання) газу зображується кривою, яка називається адіабатою.

При адіабатичному розширенні газ здійснює позитивну роботу (A > 0); тому його внутрішня енергія зменшується (ΔU < 0). Це призводить до зниження температури газу. Внаслідок цього тиск газу при адіабатичному розширенні убуває швидше, ніж при ізотермічному розширенні (рис. 2.39).

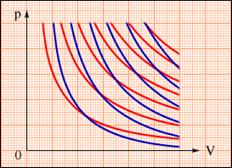
Рисунок 2.39.

Сімейства ізотерм (червоні криві) і адіабат (сині криві) ідеального газу.

Використовуючи рівняння Менделєєва-Клапейрона, можна рівняння Пуассона записати з параметрами Р і Т

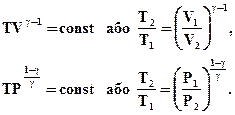(2.54)

Розрахуємо роботу, що здійснюється газом при адіабатичному процесі.

δА=- dU=- νC_v dT, А= νC_v (T₁ -Т₂).(2.55)

Використовуючи рівняння Пуассона вираз (2.55) можна записати у виді:

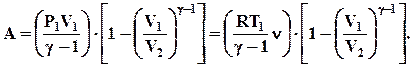(2.56)

Перший закон (початок) термодинаміки є узагальненням закону збереження і перетворення енергії для термодинамічної системи. Згідно з цим законом, енергія не може бути створена або знищена; вона передається від однієї системи до іншої і перетворюється з однієї форми в іншу. Важливим наслідком першого закону термодинаміки є твердження про неможливість створення машини, здатної здійснювати корисну роботу без споживання енергії ззовні і без яких-небудь змін усередині самої машини. Така гіпотетична машина дістала назву вічного двигуна (perpetum mobile) першого роду. Численні спроби створити таку машину незмінно закінчувалися провалом. Будь-яка машина може здійснювати позитивну роботу A над зовнішніми тілами тільки за рахунок отримання деякої кількості теплоти Q від навколишніх тіл або зменшення ΔU своєї внутрішньої енергії.

Приклади розв’язку задачі.

Кисень масою m =2 кг займає об'єм V₁ = 1 м³ і знаходиться під тиском p₁ = 0,2 МПа. Газ був нагрітий спочатку при постійному тиску до об'єму V₂ = 3 м³, а потім при постійному об'ємі до тиску p₃ = 0,5 МПа. Знайти: 1) зміну внутрішньої енергії ∆U газу; 2) виконану ним роботу A 3) кількість теплоти Q, передану газу. Побудувати графік процесу.

Дано: m=2кг V1=1 м3 V2 = 3 м3 p1 = 0,2 МПа p3 = 0,5 МПа ∆U -? A-?Q-?

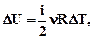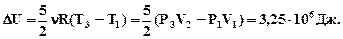
Розв’язок: Газ знаходився в трьох станах, які можна описати рівняннями, : P1V1 =nRT1 (1) , P1V2 =nRT2 (2), P3V2 =nRT3 (3)Зміна внутрішньої енергії газу рівна деΔТ=(Т3-Т1) З рівнянь (1) і (3) знайдемо Т1 і Т3, і враховуючи, що i=5, знайдемо ∆U Робота А дорівнює роботі ізобарного розширення А1, 2 =Р1(V2 - V1), оскільки на ділянці (2-3) V=const і робота дорівнює нулю. А =Р1(V2 - V1)= 0,4·106 Дж. Кількість теплоти Q=ΔU+A=3,65·106 Дж. V(м3)

Питання і задачі :

1. Що таке внутрішня енергія ідеального газу? Якими параметрами вона визначається. В результаті яких процесів вона може зміняться?

2. Що називається числом ступенів свободи молекул газу?

3. При якому процесі уся кількість теплоти, отримана газом, витрачається на збільшення внутрішньої енергії газу?

4. При якому процесі уся кількість теплоти, отримана газом, витрачається на виконання роботи проти зовнішніх сил?

5. Який газовий процес називається адіабатним? Сформулюйте перший початок термодинаміки для цього процесу. Наведіть приклади таких процесів.

6. Що таке питома і молярна теплоємності? Як розрахувати молярні теплоємності газу?

7. При ізобарному нагріванні одноатомний газ виконав роботу 139,67 Дж. Знайти зміну його внутрішньої енергії. (209,5 Дж).

8. При здійсненні газом роботи, рівної 1000 Дж, йому було передано 1500 Дж теплоти. На скільки збільшилася внутрішня енергія газу? (500 Дж).

9. При ізобарному розширенні ідеального газу, в процесі якого здійснена робота
415,5 Дж, температура газу зросла на 10 К. Знайти кількість речовини газу. (5 моль).

10. Один моль одноатомного газу нагрівається при постійному тиску. Яку кількість теплоти необхідно передати газу, щоб його об'єм подвоївся? Початкова температура газу 0°С. (5672 Дж).

11. Гелій масою m = 1 г був нагрітий на ∆T = 100 К при сталому тиску р. Визначити:
1) кількість теплоти Q, що була передана газу; 2) роботу А розширення; 3) приріст внутрішньої енергії газу ∆U.(312 Дж, 208 Дж, 520 Дж)

12. Яка доля ω₁ кількості теплоти Q₁, що підводиться до ідеального газу при ізобарному процесі, витрачається на збільшення ∆U внутрішньої енергії газу і яка доля ω₂ - витрачається на роботу А розширення? Розглянути три випадки, якщо газ: 1) одноатомний; 2) двоатомний; 3) трьохатомний. (0,4; 0,29; 0,25)

13. У циліндрі під поршнем знаходиться водень масою m = 0,02 кг при температурі
Т₁ = 300 К. Водень спочатку розширився адіабатично, збільшивши свій об'єм в п'ять разів, а потім був стиснутий ізотермічно, причому об'єм газу зменшився в п'ять разів. Знайти температуру T₂ у кінці адіабатного розширення і повну роботу A, здійснену газом. Зобразити процес графічно.(157К, 88 кДж).

14. Горюча суміш в двигуні дизеля запалюється при температурі Т₂ = 1,1 кК. Початкова температура суміші T₁ = 350 К. У скільки разів треба зменшити об'єм суміші при стискуванні, щоб вона запалилася? Стискання вважати адіабатним. Показник адіабати γ для суміші прийняти рівним 1,4. (1,75)