Незворотність теплових процесів. Другий закон термодинаміки

Перший закон термодинаміки - закон збереження енергії для теплових процесів - встановлює зв'язок між кількістю теплоти Q, отриманою системою, зміною її внутрішньої енергії ΔUі роботою A, здійсненою над зовнішніми тілами:

Q = ΔU + A.

Згідно з цим законом, енергія не може бути створена або знищена; вона передається від однієї системи до іншої і перетворюється з однієї форми в іншу. Процеси, що порушують перший закон термодинаміки, ніколи не спостерігалися. На рисунку 2.46 зображені пристрої, заборонені першим законом термодинаміки.

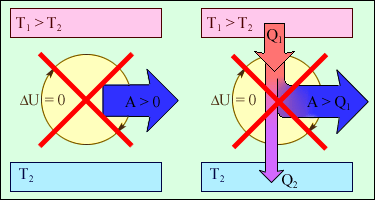
Рисунок 2.46.

1 - вічний двигун 1 роду, що здійснює роботу без споживання енергії ззовні;

2 - теплова машина з коефіцієнтом корисної дії η > 1.

Перший закон термодинаміки не встановлює напряму теплових процесів. Проте, як показує дослід, багато теплових процесів можуть протікати тільки в одному напрямі. Такі процеси називаються незворотними. Наприклад, при тепловому контакті двох тіл з різними температурами тепловий потік завжди спрямований від теплішого тіла до холоднішого. Ніколи не спостерігається самовільний процес передачі тепла від тіла з низькою температурою до тіла з вищою температурою. Отже, процес теплообміну при кінцевій різниці температур є необоротним.

Оборотними процесами називають процеси переходу системи з одного рівноважного стану в інший, які можна провести у зворотному напрямі через ту ж послідовність проміжних рівноважних станів. При цьому сама система і навколишні тіла повертаються до початкового стану.

Незворотними є процеси перетворення механічної роботи у внутрішню енергію тіла із-за наявності тертя, процеси дифузії в газах і рідинах, процеси перемішування газу за наявності початкової різниці тисків і т. д. Усі реальні процеси незворотні, але вони можуть скільки завгодно близько наближатися до зворотних процесів. Зворотні процеси є ідеалізацією реальних процесів.

Перший закон термодинаміки не може відрізнити зворотні процеси від незворотних. Він просто вимагає від термодинамічного процесу певного енергетичного балансу і нічого не говорить про те, можливий такий процес або ні. Напрям протікання процесів встановлює другий закон термодинаміки. Він може бути сформульований у вигляді заборони на певні види термодинамічних процесів.

Англійський фізик У. Кельвін дав в 1851 р. наступне формулювання другого закону:

У циклічно діючій тепловій машині неможливий процес, єдиним результатом якого було б перетворення в механічну роботу усієї кількості теплоти, отриманої від єдиного теплового резервуару.

Гіпотетичну теплову машину, в якій міг би відбуватися такий процес, називають "вічним двигуном другого роду". У земних умовах така машина могла б відбирати теплову енергію, наприклад, у Світового океану і повністю перетворювати її на роботу. Маса води у Світовому океані складає приблизно 10²¹ кг, і при її охолодженні на один градус виділилася б величезна кількість енергії (≈ 10²⁴ Дж), еквівалентна повному спалюванню 10¹⁷ кг вугілля. Енергія, що щорічно виробляється на Землі, приблизно в 10⁴ раз менше. Тому "вічний двигун другого роду" був би для людства не менш привабливий, чим "вічний двигун першого роду", заборонений першим законом термодинаміки.

Німецький фізик Р. Клаузіус дав інше формулювання другого закону термодинаміки:

Неможливий процес, єдиним результатом якого була б передача енергії шляхом теплообміну від тіла з низькою температурою до тіла з вищою температурою.

На рисунку 2.47 зображені процеси, що забороняються другим законом, але не забороняються першим законом термодинаміки. Ці процеси відповідають двом формулюванням другого закону термодинаміки.

1 – «вічний двигун другого роду»;

2 - самовільний перехід тепла від холодного тіла до теплішого «ідеальна холодильна машина».

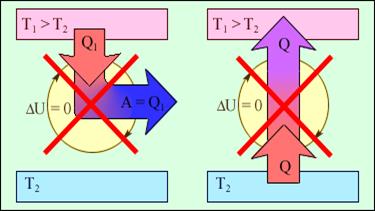
Рисунок 2.47.

На підставі будь-якого з формулювань другого закону термодинаміки можуть бути доведені наступні твердження, які називаються теоремами Карно:

1. Коефіцієнт корисної дії теплової машини, що працює при заданих значеннях температур нагрівача і холодильника, не може бути більший, ніж коефіцієнт корисної дії машини, що працює по оборотному циклу Карно при тих же значеннях температур нагрівача і холодильника.

2. Коефіцієнт корисної дії теплової машини, що працює по циклу Карно, не залежить від роду робочого тіла, а тільки від температур нагрівача і холодильника.

Таким чином, коефіцієнт корисної дії машини, що працює по циклу Карно, максимальний.

.

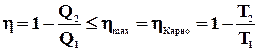Знак рівності в цьому співвідношенні відповідає зворотним циклам. Для машин, що працюють по циклу Карно, це співвідношення може бути переписане у вигляді:

.

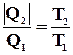У якому б напрямі не обходився цикл Карно (по, або проти годинникової стрілки) величини Q₁ і Q₂ завжди мають різні знаки. Тому можна записати

.

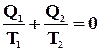Це співвідношення може бути узагальнене на будь-який замкнутий зворотний процес, який можна представити як послідовність малих ізотермічних і адіабатичних ділянок
(рис. 2.48).

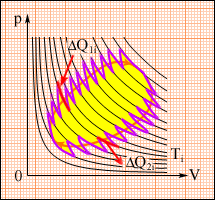
Рисунок 2.48.

Довільний оборотний цикл як послідовність малих ізотермічних і адіабатичних ділянок.

При повному обході замкнутого зворотного циклу

,

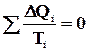де ΔQ_i = ΔQ_1i + ΔQ_2i - кількість теплоти, отримана робочим тілом на двох ізотермічних ділянках при температурі T_i. Для того, щоб такий складний цикл провести зворотним шляхом, необхідно робоче тіло приводити в тепловий контакт з багатьма тепловими резервуарами з температурами T_i.

Відношення ΔQ_i / T_i називається приведеним теплом.

Отримана формула показує, що повне приведене тепло на будь-якому зворотному циклі дорівнює нулю. Ця формула дозволяє ввести нову фізичну величину, яка називається ентропією і позначається буквою S (Р. Клаузіус, 1865 р.). Якщо термодинамічна система переходить з одного рівноважного стану в інше, то її ентропія змінюється. Різниця значень ентропії в двох станах дорівнює приведеному теплу, отриманому системою при оборотному переході з одного стану в інше.

.

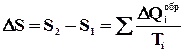У разі зворотного адіабатичного процесу ΔQ_i = 0 і, отже, ентропія S залишається незмінною.

Вираз для зміни ентропії ΔS під час переходу неізольованої системи з одного рівноважного стану (1) в інший рівноважний стан (2) може бути записаний у вигляді:

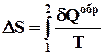. (2.65)

Ентропія визначена з точністю до постійного доданку, так само, як, наприклад, потенціальна енергія тіла в силовому полі. Фізичний зміст має різниця ΔS ентропії в двох станах системи. Щоб визначити зміну ентропії у разі незворотного переходу системи з одного стану в інший, треба придумати який-небудь зворотний процес, що зв'язує початковий і кінцевий стани, і знайти приведене тепло, отримане системою при такому переході.

Рисунок 2.49 ілюструє незворотний процес розширення газу "в порожнечу" у відсутність теплообміну. Тільки початковий і кінцевий стани газу в цьому процесі є рівноважними, і їх можна зображувати на діаграмі (p, V). Точки (a) і (b), що відповідають цим станам, лежать на одній ізотермі. Для обчислення зміни ΔS ентропії можна розглянути зворотний ізотермічний перехід (a) (b). Оскільки при ізотермічному розширенні газ отримує деяку кількість теплоти від навколишніх тіл Q > 0, можна зробити висновок, що при незворотному розширенні газу ентропія зросла: ΔS > 0.

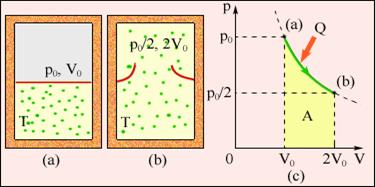
Рисунок 2.49.

Зміна ентропії де A = Q - робота газу при зворотному ізотермічному розширенні.

Інший приклад незворотного процесу - теплообмін при кінцевій різниці температур. На рисунку 2.50 зображено два тіла, поміщені в адіабатичну оболонку. Початкові температури тіл T₁ і T₂ < T₁. При теплообміні температури тіл поступово вирівнюються. Тепліше тіло віддає деяку кількість теплоти, а холодніше - отримує. Приведене тепло, що отримується холодним тілом, перевершує по модулю приведене тепло, що віддається гарячим тілом. Звідси витікає, що зміна ентропії замкнутої системи в незворотному процесі теплообміну ΔS > 0.

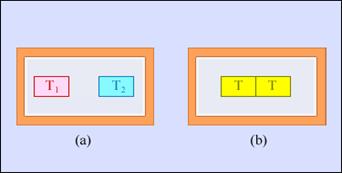
Рисунок 2.50.