Основне рівняння МКТ газів

Завдання молекулярно-кінетичної теорії полягає в тому, щоб встановити зв'язок між мікроскопічними (маса, швидкість, кінетична енергія молекул) і макроскопічними параметрами (тиск, об'єм, температура) ідеального газу.

В результаті кожного зіткнення швидкості молекул можуть змінюватися по модулю і по напряму; на інтервалах між послідовними зіткненнями молекули рухаються рівномірно і прямолінійно. У моделі ідеального газу передбачається, що усі зіткнення відбуваються за законами пружного удару, тобто підпорядковуються законам механіки.

Використовуючи модель ідеального газу, визначимо тиск газу на стінку посудини.

Взаємодію молекули із стінкою розглядаємо, як абсолютно пружний удар. В результаті проекція v_x швидкості молекули, перпендикулярна стінці, змінює свій знак на протилежний, а проекція v_y швидкості, паралельна стінці, залишається незмінною (рис.2.27). Тому зміна імпульсу молекули дорівнюватиме 2m₀v_x, де m₀ - маса молекули.

Виділимо на стінці деякий майданчик S (рис. 2.28). За час Δt з цим майданчиком зіткнуться усі молекули, що мають проекцію швидкості v_x, спрямовану у бік стінки, і знаходяться в циліндрі з площею основи S, і висотою v_xΔt.

Рисунок 2.27. Рисунок 2.28.

Нехай в одиниці об'єму посудини містяться n молекул; тоді число молекул в об'ємі циліндра становить nSv_xΔt. Але з цього числа лише половина рухається у бік стінки, а інша половина рухається в протилежному напрямі і із стінкою не стикається. Отже, число ударів молекул об майданчик S за час Δt дорівнює:

Оскільки кожна молекула при зіткненні із стінкою змінює свій імпульс на величину 2m₀v_x, то повна зміна імпульсу усіх молекул, що зіткнулися за час Δtз майданчиком S, рівна:

За законами механіки ця зміна імпульсу усіх молекул, що зіткнулися із стінкою, відбувається під дією імпульсу сили FΔt, де F - деяка середня сила, діюча на молекули з боку стінки на майданчику S. Але за 3-м законом Ньютона така ж по модулю сила діє з боку молекул на майданчик S. Тому можна записати:

Розділивши обидві частини на SΔt, отримаємо:

де Р - тиск газу на стінку посудини.

При виводі цього співвідношення передбачалося, що усі n молекул, які знаходяться в одиниці об'єму газу, мають однакові проекції швидкостей на вісь X. Насправді це не так.

Щоб уточнити формулу для тиску газу на стінку посудини, припустимо, що усі молекули розбиті на групи, n₁, n₂, n₃ і т. д. з проекціями швидкостей v_x1, v_x2, v_x3 і т. д. відповідно.

При цьому:

Кожна група молекул вносить свій вклад в тиск газу. В результаті зіткнень із стінкою молекул з різними значеннями проекцій v_xi швидкостей виникає сумарний тиск

Сума, що входить в цей вираз, - це сума квадратів проекцій v_x усіх n молекул в одиничному об'ємі газу. Якщо цю суму розділити на n, то ми отримаємо

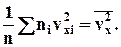
Тепер формулу для тиску газу можна записати у виді

Оскільки усі напрями для векторів швидкостей молекул рівно ймовірні, середнє значення квадратів їх проекцій на координатні осі рівні між собою:

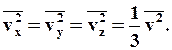
Остання рівність витікає з формули:

Формула для середнього тиску газу на стінку посудини запишеться у виді

(2.10)

Це рівняння встановлює зв'язок між тиском p ідеального газу, масою молекули m₀, концентрацією молекул n, середнім значенням квадрата швидкості і середньою кінетичною енергією E_k поступального руху молекул. Його називають основним рівнянням молекулярно-кінетичної теорії газів.

Таким чином, тиск газу дорівнює двом третинам середньої кінетичної енергії поступальної ходи молекул, що містяться в одиниці об'єму.

Температура

У основне рівняння молекулярно-кінетичної теорії газів (2.10) входить добуток концентрації молекул n на середню кінетичну енергію E_k поступального руху молекул. Якщо припустити, що газ знаходиться в посудині незмінного об'єму V, то 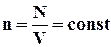(N - число молекул в посудині). В цьому випадку зміна тиску Δp пропорційна зміні ΔE_k середньої кінетичної енергії.

Виникають питання, яким чином можна на досліді змінювати середню кінетичну енергію руху молекул в посудині незмінного об'єму? Яку фізичну величину треба змінити, щоб змінилася середня кінетична енергія. Такою величиною у фізиці є температура.

Поняття температури тісно пов'язане з поняттям теплової рівноваги. Тіла, що знаходяться в контакті одне з одним, можуть обмінюватися енергією. Енергія, що передається одним тілом іншому при тепловому контакті, називається кількістю теплоти.

Теплова рівновага - це такий стан системи тіл, що знаходяться в тепловому контакті, при якому не відбувається теплопередачі від одного тіла до іншого, і усі макроскопічні параметри тіл залишаються незмінними. Температура - це фізичний параметр, однаковий для усіх тіл, що знаходяться в тепловій рівновазі. Можливість введення поняття температури виходить з досліду і носить назву нульового закону термодинаміки.

Для виміру температури використовуються фізичні прилади - термометри, в яких про величину температури судять по зміні якого-небудь фізичного параметра. Для створення термометра необхідно вибрати термометричну речовину (наприклад, ртуть або спирт) і термометричну величину, що характеризує властивість речовини (наприклад, довжина ртутного або спиртового стовпчика). У різних конструкціях термометрів використовуються різноманітні фізичні властивості речовини (наприклад, зміна лінійних розмірів твердих тіл або зміна електричного опору провідників при нагріванні).

Термометри мають бути відкалібровані. Для цього їх приводять в тепловий контакт з тілами, температури яких вважаються заданими. Найчастіше використовують прості природні системи, в яких температура залишається незмінною, незважаючи на теплообмін з довкіллям - це суміш льоду і води і суміш води і пари при кипінні при нормальному атмосферному тиску.

За температурною шкалою Цельсія точці плавлення льоду приписується температура 0°С, а точці кипіння води - 100°С. Зміна довжини стовпа рідини в капілярах термометра на одну соту довжини між відмітками 0°С і 100°С приймається рівним 1°С. У ряді країн (США) широко використовується шкала Фаренгейта (T_F), в якій температура замерзаючої води приймається рівною 32°F, а температура кипіння води 212°F. Отже,

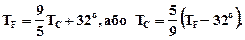
Особливе місце у фізиці займають газові термометри (рис. 2.29), в яких термометричною речовиною є розріджений газ (гелій, повітря) в посудині незмінного об'єму (V = const), а термометричною величиною - тиск газу p. Дослід показує, що тиск газу (при V = const) росте із зростанням температури, виміряної за шкалою Цельсія.

Рисунок 2.29.

Щоб проградуювати газовий термометр постійного об'єму, можна виміряти тиск при двох значеннях температури (наприклад, 0°C і 100°C), нанести точки p₀ і p₁₀₀ на графік, а потім провести між ними пряму лінію (рис. 2.30). Використовуючи отриманий таким чином калібрувальний графік, можна визначати температури, що відповідають іншим значенням тиску. Екстраполюючи графік в область низьких тисків, можна визначити деяку "гіпотетичну" температуру, при якій тиск газу став би рівним нулю. Розрахунки показують, що ця температура рівна - 273,15°С і не залежить від властивостей газу. Неможливо експериментально отримати шляхом охолодження газ з нульовим тиском, оскільки при дуже низьких температурах усі гази переходять в рідкі або тверді стани.

Рисунок 2.30.

Англійський фізик У. Кельвін в 1848 р. запропонував використовувати точку нульового тиску газу для побудови нової температурної шкали (шкала Кельвіна). У цій шкалі одиниця виміру температури така ж, як і в шкалі Цельсія, але нульова точка змінена:

T_К = T_С + 273,15.

У СІ прийнято одиницю виміру температури за шкалою Кельвіна називати кельвіном і означати буквою K. Наприклад, кімнатна температура T_С = 20 °С за шкалою Кельвіна рівна T_К = 293,15 К.

Температурна шкала Кельвіна називається абсолютною шкалою температур. Вона виявляється найбільш зручною при побудові фізичних теорій.

Таким чином, тиск розрідженого газу в посудині постійного об'єму V змінюється прямо пропорційно його абсолютній температурі: p ~ T. З іншого боку, дослід показує, що при незмінних об'ємі V і температурі T тиск газу змінюється прямо пропорційно відношенню кількості речовини ν в цій посудині до об'єму V посудини

де N - число молекул в посудині,N_A - стала Авогадро, n = N / V- концентрація молекул. Об'єднуючи ці співвідношення пропорційності, можна записати:

p = nkT,(2.11)

де k - деяка універсальна для усіх газів постійна величина. Її називають стала Больцмана, на честь австрійського фізика Л. Больцмана (1844-1906 рр.), одного з творців молекулярно-кінетичної теорії. Стала Больцмана - одна з фундаментальних фізичних констант. Її чисельне значення в СІ становить:

k = 1,38·10^–23 Дж/К.

Порівнюючи співвідношення p = nkTз основним рівнянням молекулярно-кінетичної теорії газів, можна отримати:

(2.12)

Середня кінетична енергія хаотичного руху молекул ідеального газу прямо пропорційна абсолютній температурі.

Таким чином, температура є міра середньої кінетичної енергії поступального руху молекул.