Середня довжина вільного пробігу і число зіткнень за секунду молекул газу.

Для характеристики теплового руху в газах у багатьох випадках дуже важливо знати величину середнього вільного пробігу молекул λ, тобто середню довжину шляху молекули між двома зіткненнями і середнє число зіткнень z однієї молекули за 1 секунду.

Молекули газу, знаходячись в тепловому русі, безперервно стикаються одна з одною. Мінімальна відстань, на яку зближуються при зіткненні центри двох молекул, називається ефективним діаметром молекули d.

Визначити середню довжину шляху молекули між двома зіткнення. Припустимо, що усі молекули, окрім даної, покояться. Молекула, що рухається, зіткнеться впродовж часу
τ=1 с з усіма молекулами газу, центри яких розташовані усередині циліндричного об'єму, описаного по шляху руху молекули і має радіус рівний ефективному діаметру молекули, а довжина дорівнює відносній середній швидкості молекули v_ср (рис. 2.34). Об'єм циліндра становить πd²v_ср τ. Число молекул, центри яких повинні знаходиться у вказаному об'ємі, становить nπd²v_срτ, де n - концентрація газу. Таким чином, якби усі інші молекули, окрім тієї, що розглядається, були нерухомі, те середнє число зіткнень молекул 1 секунду, було б рівне:

z=nπd²v_ср.

Рисунок. 2.34.

Насправді середнє число зіткнень має бути більше отриманої величини, так, як внаслідок руху інших молекул дана молекула отримала б деяке число зіткнень навіть у тому випадку, якщо б вона залишалася нерухомою. Точний підрахунок показує, що отриманий результат має бути помножений на 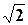, тоді

z= 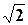n·π·d²·vср,(2.18)

а середня довжина вільного пробігу молекул дорівнює:

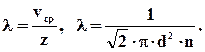(2.19)

Середня довжина вільного пробігу молекул газу за нормальних умов становить
~ 10^-7 м. При зменшенні концентрації газу середня довжина вільного пробігу збільшується.

Дифузія.

Якщо уздовж будь-якого напряму (наприклад уздовж осі Х) існує неоднорідність
густини газу, її можна характеризувати градієнтом густини.

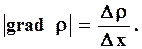
В такому не врівноваженому стані відбувається перенесення (дифузія) маси газу. Закон дифузії був отриманий німецьким фізиком Фіком. Цей закон виражається формулою.

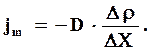(2.20)

де j_m - густина потоку маси дифундуючої речовини, що проходить в одиницю часу через одиничний майданчик, перпендикулярний осі Х. Знак мінус показує, що перенесення маси відбувається у напрямі убування густини.

У загальнішому вигляді закон Фіка може бути виражений формулою:

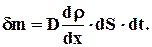(2.21)

Маса дифундуючої речовини δmпропорційна часу dt, площі dS і градієнту густини
| grad ρ|.

D - коефіцієнт дифузії. Коефіцієнт дифузії чисельно дорівнює масі дифундуючої речовини, що пройшла через одиницю площі за одиницю часу при градієнті густини, рівному одиниці.

Згідно кінетичної теорії газів.

(2.22)

Для різних газів за нормальних умов коефіцієнт дифузії має значення приблизно від 10^-5 до 10^-4 м²/с. Так, як середня швидкість v_ср пропорційна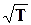, то при збільшенні температури швидкість дифузії збільшується.

Теплопровідність

Дослідним шляхом встановлено, якщо в якомусь середовищі уздовж деякого напряму Х температура не залишається постійною, то уздовж цього напряму встановлюється потік тепла.

У загальному випадку повну характеристику зміни температури уздовж напряму Х отримаємо, якщо знатимемо швидкість зміни температури або градієнт температури уздовж осі Х :

Відмітимо, що температура скалярна величина, але градієнт температури це вектор, спрямований у бік збільшення температури. Користуючись поняттям про градієнт температури, можна написати рівняння теплопровідності:

(2.23)

Де J_E - густина теплового потоку - енергія, яка переноситься у формі теплоти в одиницю часу через одиничний майданчик , c- коефіцієнт теплопровідності. Знак мінус показує, що потік енергії має напрям, протилежний до напряму градієнта температури.

Точний підрахунок явищ теплопровідності проводиться на основі закону Фур'є: кількість тепла δQ, що проходить за проміжок часу dt через елементарний майданчик dS, перпендикулярний лінії, уздовж якої тече потік енергії, пропорційний часу dt, площі dS і градієнту температури .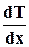

. (2.24)

Коефіцієнт теплопровідності може бути визначений як кількість тепла, яке протікає через одиницю площі за одиницю часу при градієнті температури рівному одиниці.

Речовини, для яких коефіцієнт теплопровідності має велике значення, називають хорошими провідниками теплоти, а ті, для яких χ має малі значення, - поганими провідниками тепла. Кращими провідниками є метали, гірше проводять дерево, скло, рослинні тканини. Поганими провідниками тепла є гази і рідини (за винятком рідких металів). Згідно кінетичної теорії газів коефіцієнт теплопровідності рівний:

(2.25)

де r - густина газу, с_v - питома теплоємність газу при постійному об'ємі.