Determining the principal stresses and the principal planes position

Let us consider the reverse problem. The normal and shearing stresses acting on the element plane are given (Fig. 2.8 a). It is necessary to determine the principal planes positions and the principal stress values. Let us consider the trihedral prism with the ABC base (Fig. 2.8 b). Take 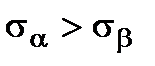. The angle 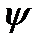will be counted off from the larger stress direction until the normal to the plane. We will take the against the clock direction as positive. The inclined plane area will be denoted by dA. Then, the vertical plane area will be 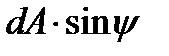and the horizontal one will be - .

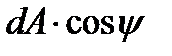Projecting all forces on the direction 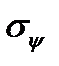, we get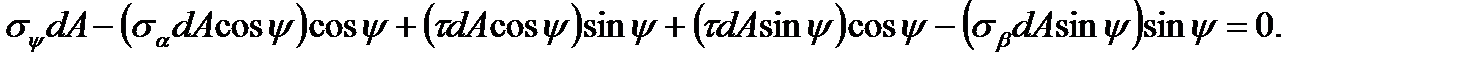

Now we will project all forces on the 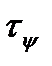direction:

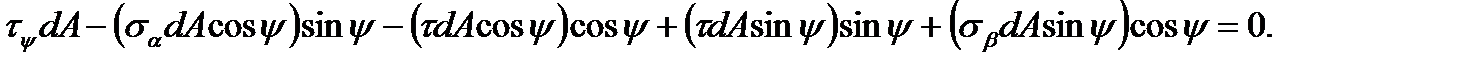
Having cancelled by dA introducing the function of double angles, we get

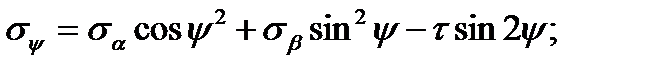(2.11)

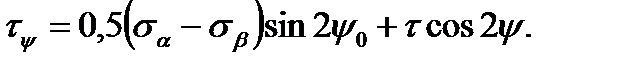(2.12)

a) b)

σα

σα

σβ

σβ

τ

τ

τ

τ

ψ

ψ

σψ

τψ

τ

σβ

σα

τα

Fig. 2.8.

The 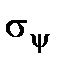value is continuously changing with the angle change of the y plane incline. To find the principal planes position we have to equal the 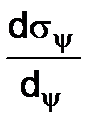derivative to zero, then we get:

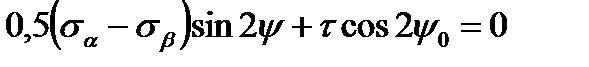
After the transposition we have

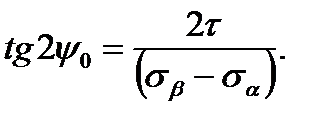(2.13)

We get the formulae of the principal stresses determination when to use double angle functions are applied to transpose:

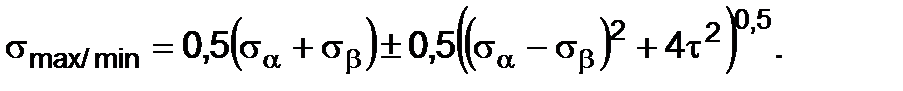(2. 14)

The shearing stresses on the principal plane are always equal to zero.

2.12. The relation between the deformations and the stresses for the plane and general stresses (a general form of Hook^’s law)

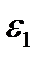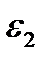Determine the and deformations for the plane stress in the principal stress directions (Fig. 2.9).For this Hook’s law is used in the unaxial state of stress.

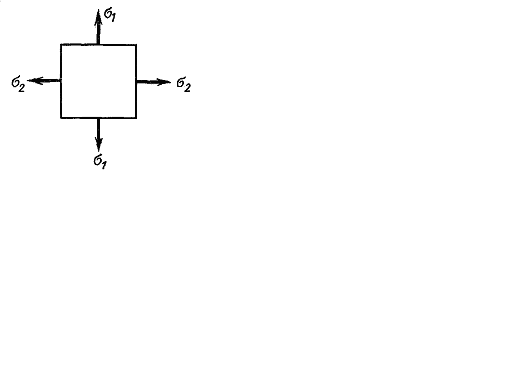
Fig. 2.9.

The 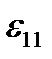unit strain in the vertical direction under the action of the 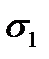stress in equal to

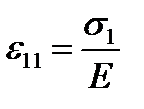.(2.15)

and simultaneously the unit lateral strain in the horizontal direction is equal to

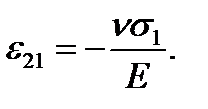(2.16)

Under the action of 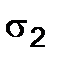alone we have the elongation 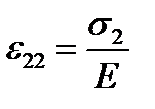in the horizontal direction and the contraction 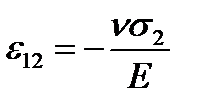in the vertical direction (n - Poisson^’s ratio).

Summing up the deformations we get

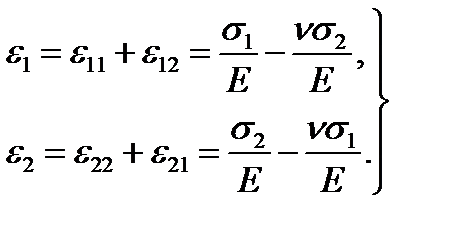(2.17)

The formulas express the general form of Hook^’s law of the plane stress.

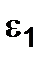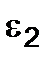If the and deformations are known, solving the equation (2.17) then we get the following formulas:

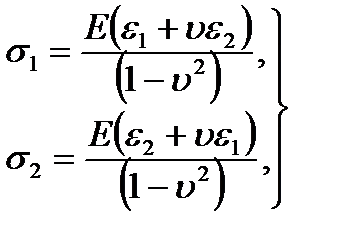(2.18)

Analogously for the volumetric stress (the three 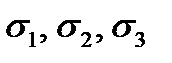principal stresses are not equal to zero) we get

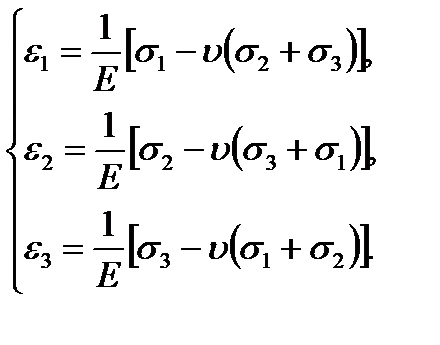(2.19)

The equations (2.19) are the general form of Hook^’s law for the general state of stress. The deformations in the principal stress directions are called principal strains.

We can determine the volume change under deforming if 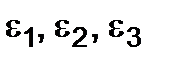are known. Take a cube with the 1 cm dimensions. Its volume before deforming equals 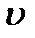=1 сm³. The volume after deforming is equal to 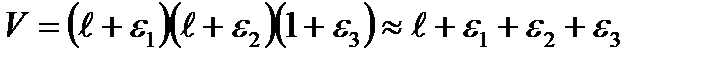(the 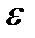products are ignored since they are small compared with ).

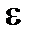The unit volume change:

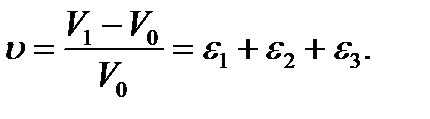(2.20)

Substituting the 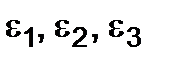values, we get

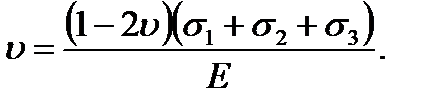(2.21)

From the formula (2.20) it follows that Poisson’s ratio cannot be more than 0,5.