Determination of stresses at the inclined sections in tension (compression) in two directions

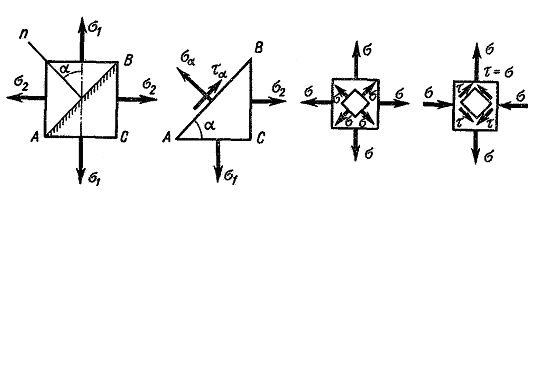
Let us consider a general case of the plane stress state, when two principal stresses ( 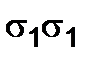in Fig. 2.7 a) differ from zero.

The indices for denoting the principal stresses are put so as the 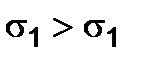inequality is observed. We shall count off the positive 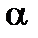angle between the direction and the normal to the arbitrary section against the clock.

The angle between the 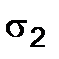stress direction and the plane is equal to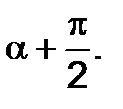

The 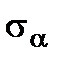and 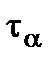stresses at the arbitrary inclined section can be determined from the equilibrium condition of the ABC trihedral prism (Fig. 2.7 b) or calculated by the formulae (2.3) and (2.4) by summing the stresses caused by 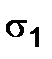and the stresses caused by 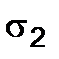. As a result we get

a) b) c) d)

Fig. 2.7.

wherefrom

(2.8)

further,

wherefrom

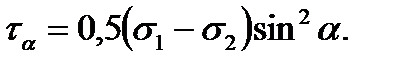(2.9)

From the formula (2.9) it is evident that the maximum shearing stresses are equal to half the difference of the principal stresses:

. (2.10)

Special cases.

The first case. Let us consider the stress state, under which 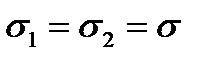(Fig. 2.7 c).

In this case for all sections passing through the point under study the shearing stress is equal to zero, and the normal stress has the same value 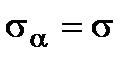. That kind of the stress state is called the uniform plane tension (or compression).

The second case. Let us consider the stress state as presented in Fig. 2.7 d, characterized by the principal stresses 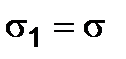and 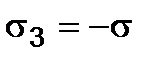. Then, .

Determine the stresses at the sections having the same slope to the directions 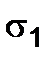and 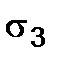i.e. at 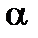= 45° and 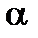= 135°.

We get 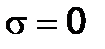; 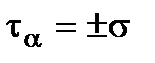by the formulae (2.8) and (2.9). This stress state is called the pure shear.