Polar moment of inertia

The Polar moment of inertia of the plane figure about a pole in the plane is called the sum of the products of the elements of the area and the square of the distance between the element and the pole for all the figure area (Fig. 3.2).

Polar moment of inertia is denoted by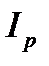

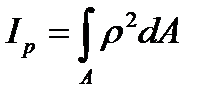. (3.5)

The unit of the polar moment of inertia is the unit of length.

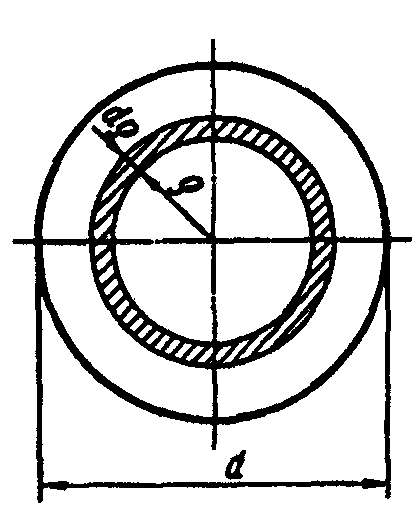
Fig. 3.2.

The Polar moment of inertia is always a positive value and is not equal to zero.

Since we shall need the concept of the polar moment of inertia to study the torsion deformation of the round shaft, we derive formulas to determine the polar moment of inertia of the round solid and circular sections taking the centers of these figures as the pole.

1. The circle has the diameter d (Fig. 3.2). Let us remove the infinite small area dA of the ring shape with the dr width lying from the pole (r is the variable value) at the r distance. Thus, 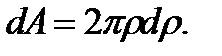Determine the polar moment of inertia:

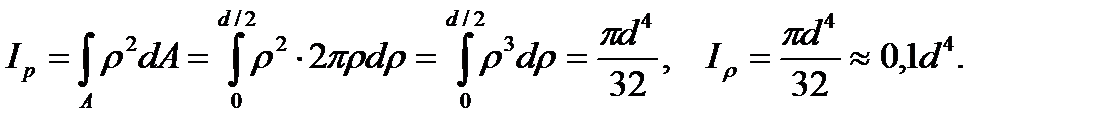(3.6)

2. The ring with the dimensions Dxd:

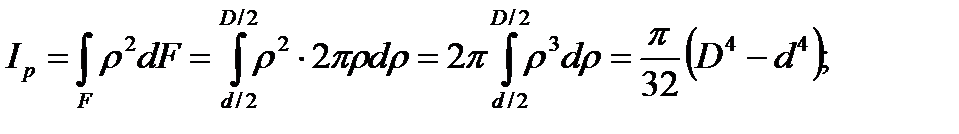
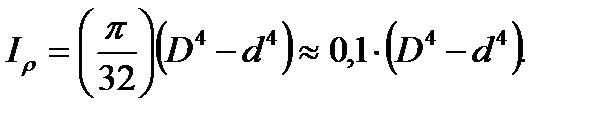(3.7)

The Polar moment of inertia of the ring section can be determined as the difference of the polar moment of inertia of large and small circles.