Determining the internal forces by the method of sections. Stresses

The method of sections consists in that a body is cut by an imagining plane into two parts, one part is removed, and internal forces acting before the cutting are applied to the section of the remained part; the remaining portion of the body is considered as a separate body being in equilibrium under the external and internal forces applied to this section.

The method of sections is based on Newton^’s third law.

remaining portion

removed portion

F2

F1

F1

F2

m1

m1

a     a

y a   a

m2

F4

F3

Q

a Fr

N

Mb

z

M¢b

F¢r

a     a

F4

m2

Q

F3

Fig. 1.1.

We can find the resultant of these forces by applying the equilibrium condition to the remaining body portion.

The bar is the basic calculating object in the strength of materials. Let us consider the static resultant of the internal forces in a bar cross section. Cut a bar by the cross section a-a and consider the equilibrium of its left portion (Fig.1.1).

The resultant force vector F_r applied in the centroid of the area and the resultant moment M_r = M_b (they balance the external force plane system applied to the remaining beam portion) are the static resultants of internal forces in the general case which act at the section a-a, if the external forces, applied to the bar, are in one plane.

Let us decompose the resultant force vector into the component N directed along the bar axis and the component Q perpendicular to this axis i.e. the axis lying at the cross-section plane.

These components of the resultant force vector and the resultant moment are called internal forces factors acting at a cross section of a bar. The component N is called the axial force, the component Q is called the shearing force and the couple forces with M_b are the bending moment.

Statics gives three eguations for the remaining bar portion to determine three pointed internal forces, namely:

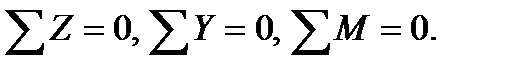
(Z – is the axis always directed along the bar).

If the external forces acting at the bar do not lie in the same plane i.e. they form the spatial force system, then in the general case there arise six internal forces factors in the cross section. To determine these statics gives six equilibrium equations (Fig.1.2):

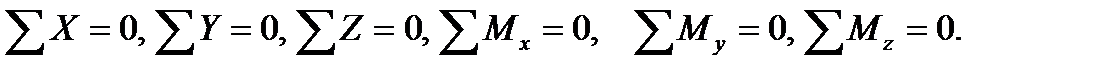
Mby

Mt

x

N

z

Mbx

Qx

Qy

y

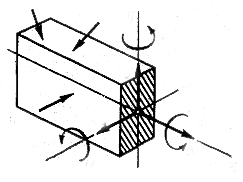
Fig. 1.2.

The six internal forces factors arising at the bar cross section in a most general case are given the following names: N is an axial force; Q_x, Q_y are shearing forces; M_t is a twisting moment; M_bx, M_by are bending moments.

There arise different internal forces factors at the bar cross section under different deformations. Consider the following special cases:

1. There is only an axial force N at the section. In this case we have a tension deformation (if the force is directed from the section) or a compression deformation (if the force is directed to the section).

2. There is only a shearing force Q, in this case we have a shear deformation.

3. There is only a twisting moment M_t. In this case we have a torsional deformation.

4. There is only a bending moment M_b. In this case we have a pure bending deformation. When a section has a simultaneous bending moment M_b and a simultaneous shearing force Q, the bend is called cross-bending.

5. When a section has some internal forces factors simultaneously (for example, a bending and a twisting moments or a bending moment and an axial force), then there is a combination of the basic deformations (combined stress).

The stress is one of basic concepts of the strength of materials.