Law of the shearing stresses couple

Let us determine normal and shearing stresses at two mutually perpendicular planes.

For the inclined under 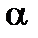angle plane by the formulae (2.3) and (2.4) we have:

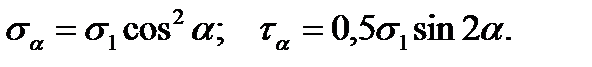
For the mutually perpendicular plane under 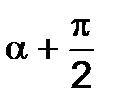angle value, we can determine the normal and shearing stresses either from the equilibrium condition of the upper or lower bar parts (Fig.2.6 c) or by the formulae (2.3) and (2.4) replacing 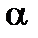by .

To study the material mechanical properties irrespective of the specimen dimensions a diagram in the coordinates “stress - deformation” 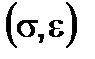is applied. The diagrams in question differ only by scales.

Applying the formulae (2.3) and (2.4), we get

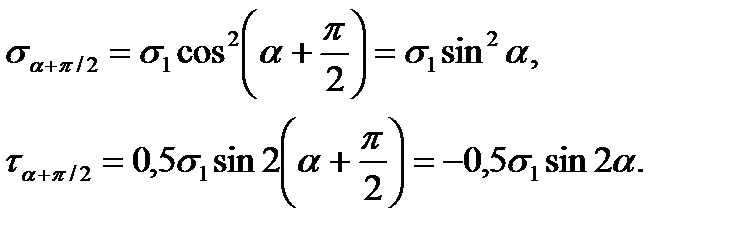
Analyzing the obtained results we can see that, firstly,

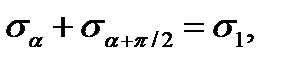
i.e. the sum of the normal stresses in two mutually perpendicular areas is constant and equal to the principal stress, secondly,

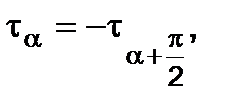
So, at two mutually perpendicular areas shearing stresses (law of the shearing stresses couple) equal by value and reverse at their signs act.

The law of shearing stresses couple (reciprocation) is valid not only for the monoaxial, but for any other tensed condition: biaxial and volumetric.