Вращающиеся и работающие на кручение стержни называют валами.

Вместо аксонометрического изображения будем применять главным образом, плоское, как более простое. Внешние скручивающие моменты и внутренние крутящие моменты будем изображать в виде линии с двумя кружочками. В одном из них будем ставить точку, обозначающую начало стрелки (на нас), а в другом - крестик, обозначающий конец стрелки, направленный от нас (рис. 4.2).

Для определения крутящих моментов Т, возникающих в сечениях вала под действием внешних скручивающих моментов или поперечной нагрузки, будем применять метод сечений. Сделаем мысленный разрез стержня (рис. 4.2), например по а-а, отбросим одну часть стержня, в данном случае левую, и рассмотрим равновесие оставшейся правой части. Взаимодействие частей стержня заменим крутящим моментом Т, уравновешивающим внешний момент Т_е. Для равновесия отсеченной части необходимо, чтобы алгебраическая сумма всех моментов, действующих на нее, была равна нулю. Отсюда в рассматриваемом случае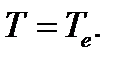

Если на отсеченную часть будет действовать несколько внешних моментов, то, проведя аналогичные рассуждения можно убедиться, что крутящий момент в сечении численно равен алгебраической сумме внешних скручивающих моментов, действующих по одну сторону от сечения.

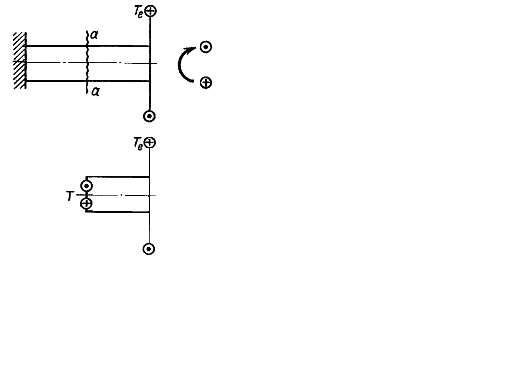
Рис. 4.2.

Для наглядного представления о характере распределения и значений крутящих моментов по длине стержня строят эпюры (графики) этих моментов. Построение их вполне аналогично построению эпюр продольных сил при растяжении или сжатии. Для построения эпюр необходимо условиться о правиле знаков. Общепринятого правила знаков для крутящих моментов не существует. Может быть принято любое правило знаков. Важно лишь принятое правило выдержать на всем протяжении эпюры.

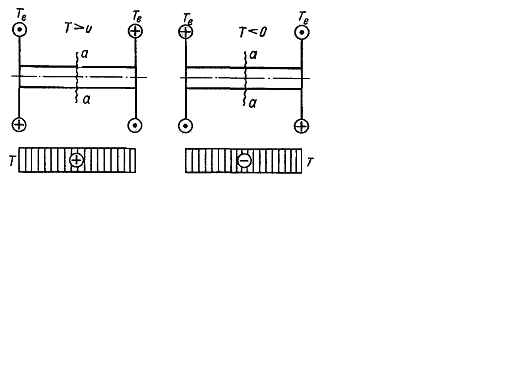
Рис. 4.3.

Примем следующее правило знаков (рис. 4.3). Крутящий момент в сечении а-а считаетсяположительным, когда внешний момент вращает отсеченную часть против часовой стрелки, если смотреть на отсеченную часть со сторона сечения. Если же внешний момент вращает отсеченную часть по часовой стрелке (при взгляде со стороны сечения), то крутящий момент в сечениибудем считать отрицательным, построение эпюры крутящих моментов поясним на следующем примере (рис. 4.4). Рассмотрим вал CD, опирающийся на подшипники В и А и находящийся в равновесии под действием приложенных к нему в сечениях Е, К и L моментов. Сделав сечение а-а где-либо на участке DL и рассмотрев равновесие правой отсеченной части, убедимся, что Т = 0. Если мы сделаем затем сечение b-b в любом месте участка LK, то из условия равновесия правой от сечения части получим T = 20 кНм.

Момент считаем положительным в соответствии с принятым правилом знаков. Сделав сечение с-с на участке КЕ, из условия равновесия правой части получим 20 - 30 -Т= 0, откуда Т= -10 кНм.

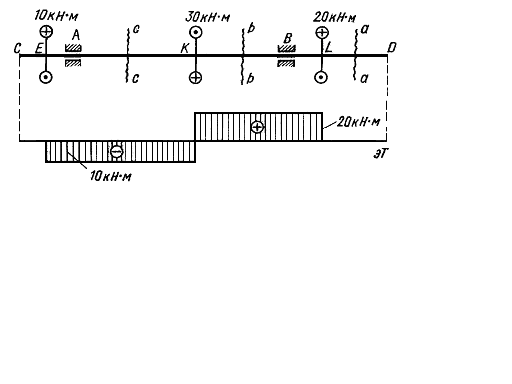
Рис. 4.4.

Получившаяся эпюра имеет форму двух прямоугольников. Важно заметить, что в местах приложения внешних моментов ординаты эпюры скачкообразно изменяются на величину приложенного здесь внешнего момента.