Осевой момент инерции

Осевым моментом инерции плоской фигуры относительно оси, лежащей в той же плоскости, называется взятая по всей площади сумма произведений площадей элементарных площадок на квадрат расстояний от них до этой оси (рис. 3.1).

Осевой момент инерции обозначим I с индексом, соответствующим оси:

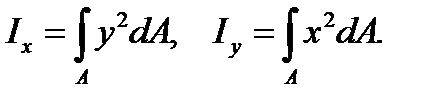(3.8)

Очевидно, что осевой и полярный моменты инерции выражаются в одинаковых единицах - (ед. длины).

Осевой момент инерции - величина всегда положительная и не равная нулю.

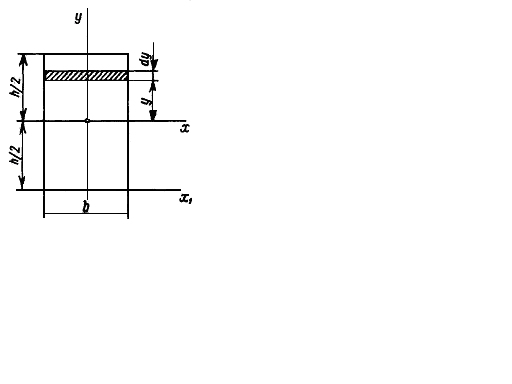
Рис.3.3.
Сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей равна полярному моменту инерции относительно начала координат:

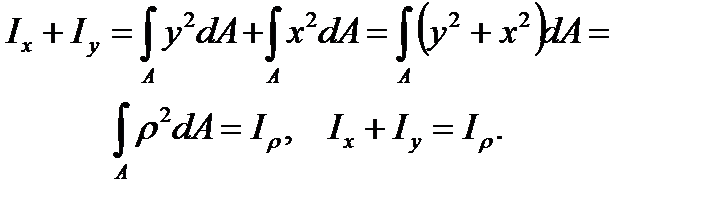(3.9)

Так как интеграл суммы равен сумме интегралов, то момент инерции сложной фигуры можно вычислять как сумму моментов инерции простых фигур, на которые разбивают сложную фигуру. Понятие об осевых моментах инерции понадобится нам в дальнейшем при изучении теории изгиба. Вычислим осевые моменты инерции некоторых простых фигур.

1. Прямоугольниксо сторонами в и h (рис. 3.3).

Бесконечно малую площадку dA выделим в виде полоски шириной в и высотой dy, тогда dA = bdy:

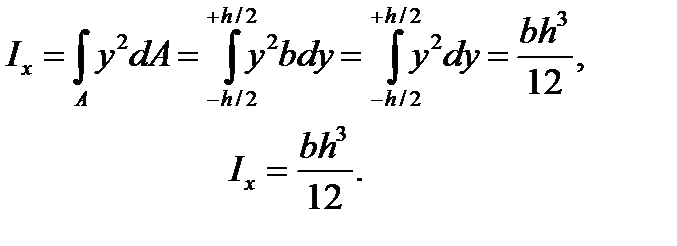(3.10)

Для квадрата со сторонойа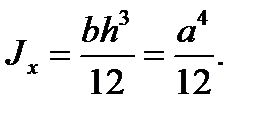

2. Круг диаметром d относительно осей x и у. В силу симметрии для круга 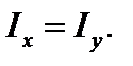, так как

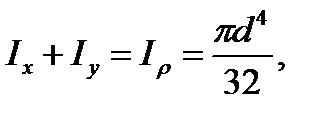
то

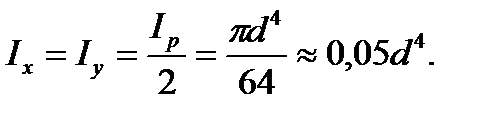(3.11)

3. Кольцо размером D х d относительно осей х и у:

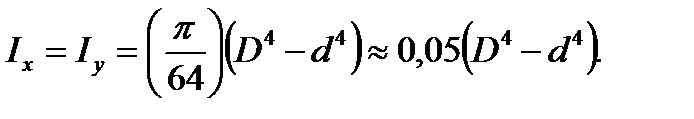(3.12)