Полярный момент инерции

Полярным моментом инерции плоской фигуры относительно полюса, лежащего в той же плоскости, называется взятая по всей площади сумма произведений площадей элементарных площадок на квадраты их расстояний до полюса (рис. 3.2).

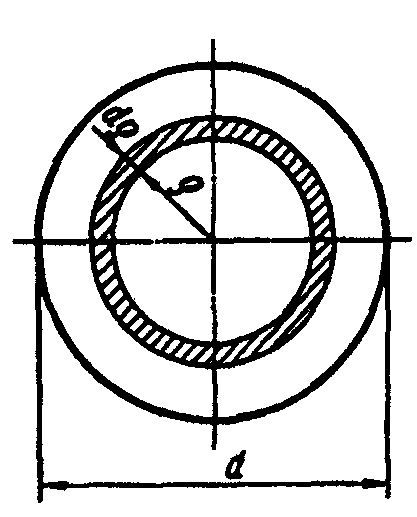
Рис. 3.2.

Полярный момент инерции обозначим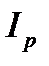

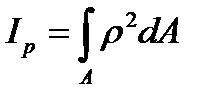. (3.5)

Единица полярного момента инерции - (ед. длины)⁴.

Полярный момент инерции – величина всегда положительная и не равная нулю.

Так как понятие полярного момента инерции понадобится нам при изучении деформаций кручения круглых валов, то выведем формулы для определения полярных моментов инерции круглого сплошного и кольцевого сечений, принимая за полюс центры этих фигур.

1. Круг диаметром d (рис. 3.2). Выделим бесконечно малую площадку dA в виде кольца шириной dr, находящегося на расстоянии r от

полюса (ρ - переменная величина). Тогда 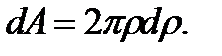Вычислим полярный момент инерции:

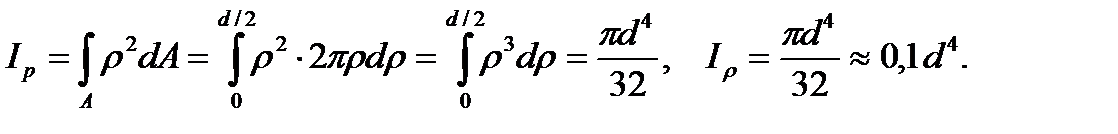(3.6)

2.Кольцо размерами D^.xd:

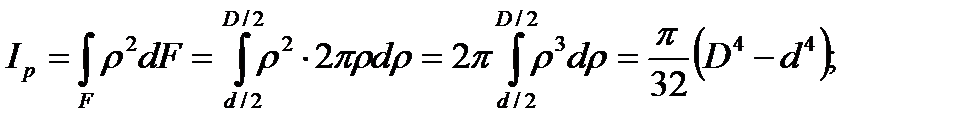
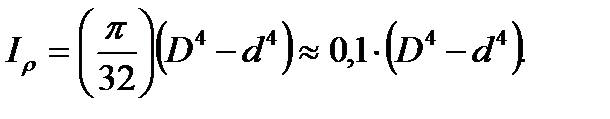(3.7)

Полярный момент инерции кольцевого сечения можно вычислить как разность полярных моментов инерции большого и малого кругов.