Зависимость между деформациями и напряжениями при плоском и объемном напряженных состояниях (обобщенный закон Гука)

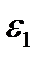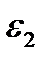Определим деформации и в направлениях главных напряжений при плоском напряженном состоянии (рис. 2.9). Для этого используем закон Гука для одноосного напряженного состояния.

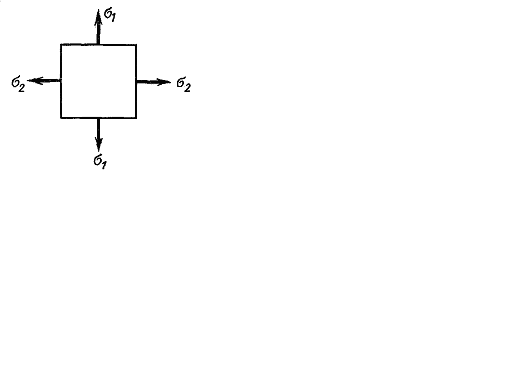
Рис. 2.9.

От действия одного напряжения 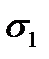относительное удлинение 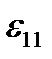по вертикали равно

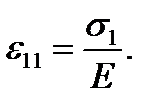(2.15)

и одновременно в горизонтальном направлении относительное сужение равно

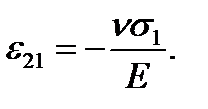(2.16)

От действия одного только 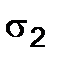имели бы в горизонтальном направлении удлинение 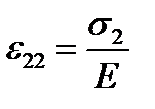и в вертикальном направлении – сужение 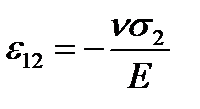: ( 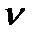– коэффициент поперечной деформации).

Суммируя деформации, получаем

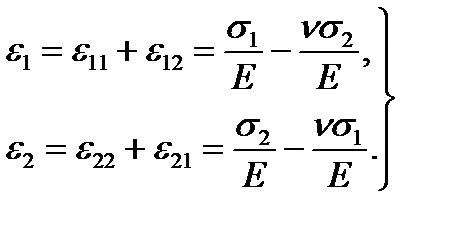(2.17)

Эти формулы выражают обобщенный закон Гука для плоского напряженного состояния.

Если известны деформаци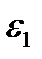и и 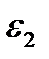то, решая уравнения - (2.17) относительно напряжени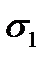й и 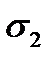получим следующие формулы:

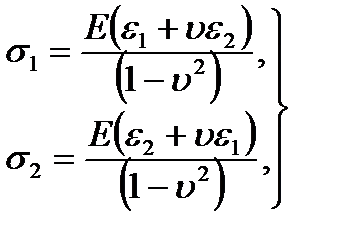(2.18)

Аналогично, для объемного (пространственного) напряженного состояния, когда все три главных напряжения 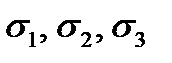отличны от нуля, получим

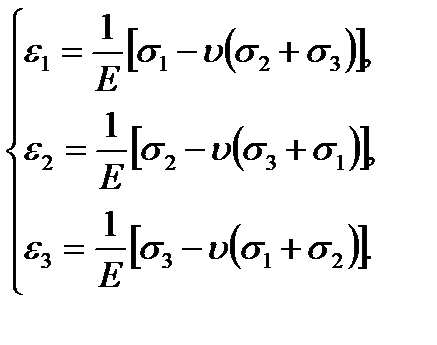(2.19)

Уравнения (2.19) представляют собой обобщенный закон Гука для объемного напряженного состояния. Деформации в направлении главных напряжений называются главными деформациями.

Зная 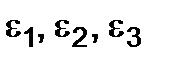, можно вычислить изменение объема при деформации. Возьмем кубик 1´1´1 см. Объем его до деформации 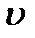=1 см³. Объем после деформации 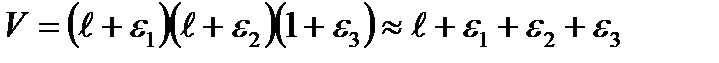(произведениями 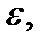как величинами малыми по сравнению с самими ε, пренебрегаем).

Относительное изменение объема:

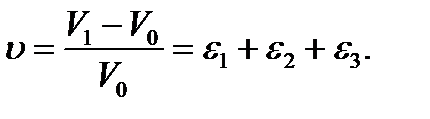(2.20)

Подставив значения 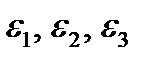, получим:

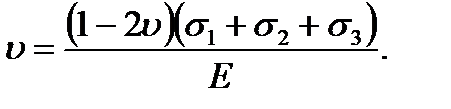(2.21)

Из формулы (2.20) следует, что коэффициент Пуассона 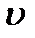не может быть больше 0,5.