Определение напряжений в наклонных сечениях при растяжении (сжатии) в двух направлениях

Рассмотрим общий случай плоского напряженного состояния, когда отличны от нуля два главных напряжения ( 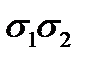на рис. 2.7 a).

Индексы у обозначений главных напряжений ставятся так, что соблюдается неравенство 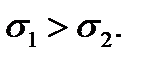Положительный угол между направлением 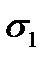и нормалью к произвольной площадке будет отсчитываться против часовой стрелки.

Между направлением напряжения 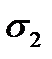и площадкой угол равен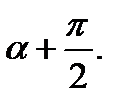

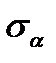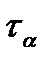Напряжения и в произвольном наклонном сечении можно или определить из условий равновесия трехгранной призмы AВС (рис. 2.7 б), или вычислить по формулам (2.3) и (2.4), суммируя напряжения от действия 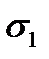с напряжениями от действия 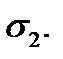В результате получим

а) б) в) г)

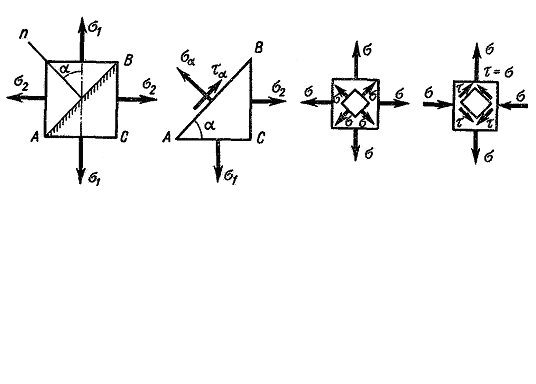
Рис. 2.7.

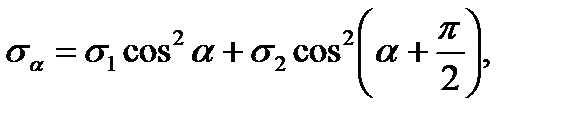
откуда

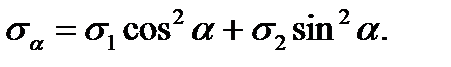(2.8)

Далее,

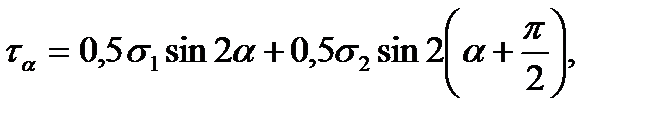
откуда

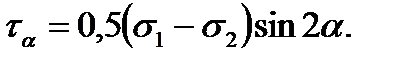(2.9)

Из формулы (2.9) видно, что максимальные касательные напряжения равны полуразности главных напряжений:

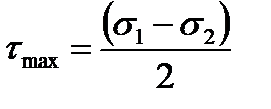. (2.10)

Частные случаи.

1-й случай. Рассмотрим напряженное состояние, при котором 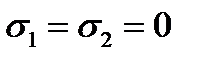(рис. 2.7 в).

В этом случае на всех площадках, проходящих через исследуемую точку, касательное напряжение 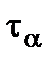равно нулю, а нормальное напряжение имеет одно и то же значение 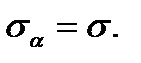Такое напряженное состояние называется равномерным двухосным растяжением (или сжатием).

2-й случай. Рассмотрим напряженное состояние, представленное на рис. 2.7 г, характеризующееся главными напряжениям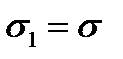и и 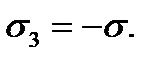При этом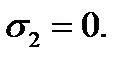

Определим напряжения в сечениях, одинаково наклоненных к направлениям 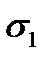и 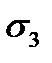, то есть пр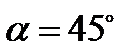и и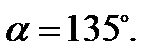

По формулам (2.8) и (2.9) получим 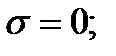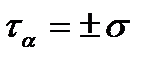, такое напряженное состояние называется чистым сдвигом.