Статический момент площади

При некоторых деформациях прочность деталей зависит не только от площади поперечного сечения, но и от его формы. До сих пор мы изучали деформации, у которых напряжения зависели только от площади поперечного сечения. В дальнейшем для изучения деформаций кручения и изгиба нам потребуется знание некоторых других геометрических характеристик плоских фигур.

Статическим моментом площади плоской фигуры относительно оси, лежащей в той же плоскости, называется взятая по всей площади сумма произведений площадей элементарных площадок на расстояния от них до этой оси (рис. 3.1).

Статический момент площади обозначим S с индексом соответствующей оси:

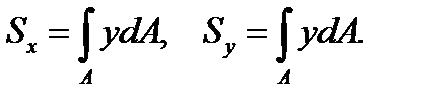(3.1)

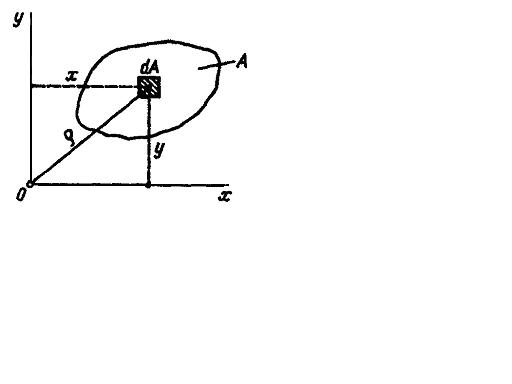
Рис. 3.1.

Формулы для определения координат центра тяжести площади фигуры:

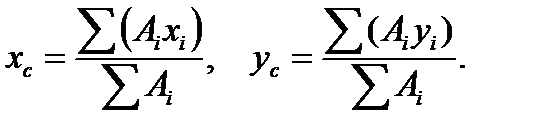(3.2)

Так как в формулах (3.2) под А можно понимать площадь dA элементарной площадки, то в пределе при dA, стремящемся к нулю, выражения, стоящие в числителях правых частей формул, будут представлять собой статические моменты площади фигуры относительно осей у и х, а 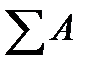, есть площадь А всей фигуры. Следовательно,

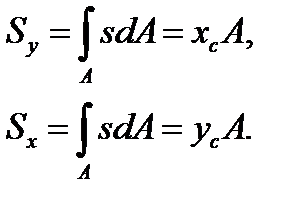(3.3)

Единица статического момента площади - (единицы длины)³.

Статический момент площади фигуры может быть величиной положительной, отрицательной и равной нулю. Очевидно, что статический момент площади относительно оси, проходящей через центр тяжести площади фигуры (центральной оси), в том числе относительно оси симметрии фигуры, равен нулю.

В формулах для определения координат центра тяжести площади под А, можно понимать площади конечных частей фигуры, а под х и у - координаты центров тяжести этих частей (т. е. применять метод разбиения). Отсюда следует, что при определении статического момента площади сложной фигуры также можно применять метод разбиения, т. е. определять статический момент всей фигуры как алгебраическую сумму статических моментов отдельных ее частей:

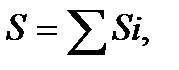(3.4)

где Si– статический момент площади каждой части фигуры.