Определение главных напряжений и положения главных площадок

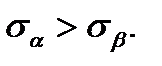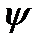Рассмотрим обратную задачу. Даны нормальные и касательные напряжения, действующие по граням элемента (рис. 2.8 а). Требуется определить положение главных площадок и значения главных напряжений. Рассмотрим равновесие трехгранной призмы с основанием ABC (рис. 2.8 б). Примем, что Угол будем отсчитывать от направления большего напряжения до нормали к площадке. За положительное направление отсчётов угла 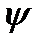примем направление против часовой стрелки. Площадь наклонной грани обозначим dA. Тогда площадь вертикальной грани будет 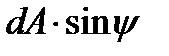, а горизонтальной - .

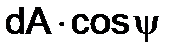Проецируя все силы на направление 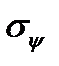, получим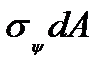

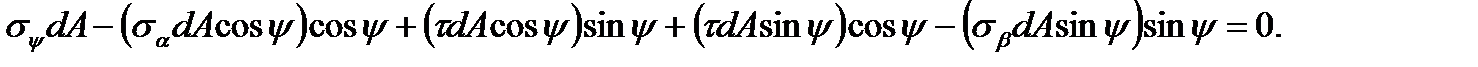
Проецируем теперь все силы на направление :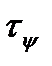

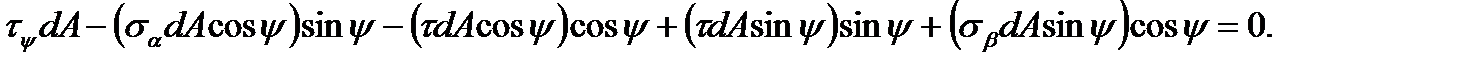
Сократив на dA и введя функции двойных углов, получим:

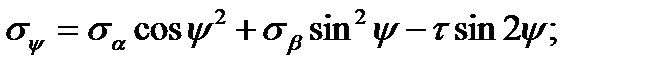(2.11)

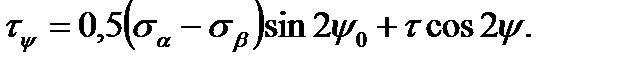(2.12)

а) б)

σα

σα

σβ

σβ

τ

τ

τ

τ

ψ

ψ

σψ

τψ

τ

σβ

σα

τα

Рис. 2.8.

При изменении угла наклона площадки 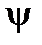величина 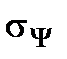непрерывно меняется. Для отыскания положения главных площадок следует приравнять производную 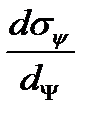нулю, тогда получим

.

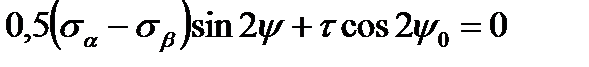После преобразования получим

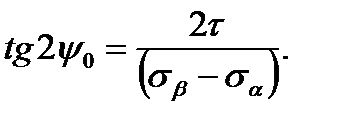(2.13)

С использованием функций двойного угла получим формулы для определения главных напряжений:

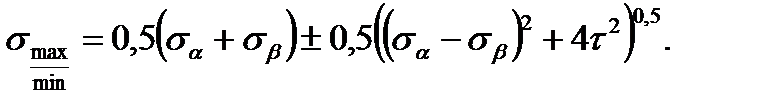(2.14)

Касательные напряжения на главных площадках всегда равны нулю.