Геометрическое представление сигналов

Идеи функционального анализа дали возможность создать теорию сигналов, в основе которой лежит представление сигнала как вектора в некотором бесконечномерном пространстве.

Если имеется некая совокупность сигналов s₁(t), s₂(t) и т. д., имеющих некоторые общие свойства, то их можно объединить в некоторое множество сигналов М = {s₁(t), s₂(t), …}.

Задача разложения сигнала сложной формы на простейшие составляющие сходна с разложением обычного вектора х трехмерного пространства на его составляющие по координатному базису единичных ортогональных векторов i, j, k. Такое представление можно записать как

x = х₁i + х₂ j + x₃k (2.6)

Составляющими вектора х по базису (i, j, k) будут векторы х₁·i, х₂·j, x₃·k. Коэффициенты х₁, х₂, х₃ представляют собой проекции вектора х на координатные оси i, j, k и называются координатами вектора х. Иначе говоря, вектор х в трехмерном пространстве полностью определяется совокупностью его координат х = (х₁, х₂, х₃).

Чтобы перейти к обобщению понятия вектора трехмерного пространства для случая n-мерного пространства, функцию x(t) по аналогии с (2.6) можно представить в виде суммы

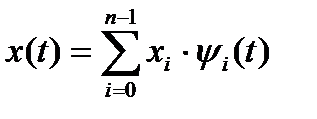, (2.7)

где ψ_i – элементарные базисные функции.

Множество векторов {ψ_i} называется линейно независимым (базисом), если условие 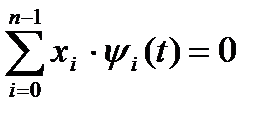выполняется лишь тогда, когда все х_i = 0.

Линейно независимые векторы {ψ_i} можно рассматривать как координатные оси пространства.

Метрическим называется линейное пространство, в котором определено расстояние между элементами (векторами) пространства (метрика), т.е. каждой паре элементов, скажем, х и у может быть поставлено в соответствие некоторое вещественное неотрицательное число d(х, у) и способ, в соответствии с которым находится это число.

Среди линейных метрических пространств важное место занимают нормированные пространства.

Для этого вводится новое понятие, соответствующее длине вектора. В математике длину вектора называют его нормой. Пространство сигналов называется нормированным, если каждому вектору s(t) однозначно сопоставлено число || s ||, называемое нормой. Для вещественных аналоговых сигналов в теории сигналов норму сигнала вводят в виде

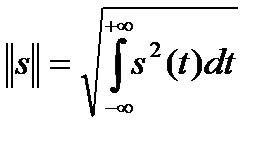. (2.8)

Для комплексных сигналов норма сигнала представляется

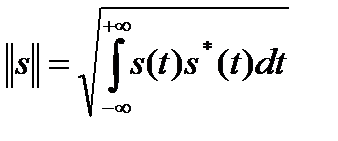. (2.9)

Квадрат нормы называется энергией сигнала E_s

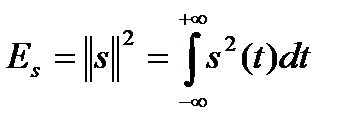. (2.10)

Такая энергия сигнала выделяется на резисторе с сопротивлением 1 Ом. Выражение (2.10) представляется очень удобным, так как отпадает необходимость расшифровывать размерность сигнала, т. е. сигнал задан в виде тока или напряжения.