Интервалы прогноза по линейному уравнению регрессии

Прогнозирование по уравнению регрессии представляет собой подстановку в уравнение регрессии соответственного значения х. Такой прогноз 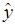называется точечным. Он не является точным, поэтому дополняется расчетом стандартной ошибки 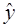; получается интервальная оценка прогнозного значения :

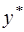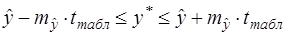
(30)

Преобразуем уравнение регрессии:

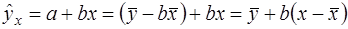
ошибка 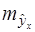зависит от ошибки 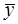и ошибки коэффициента регрессии 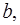то есть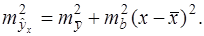

Из теории выборки известно, что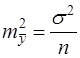

Используем в качестве оценки 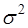остаточную дисперсию на одну степень свободы 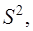получаем: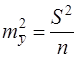

Ошибка коэффициента регрессии из формулы (20):

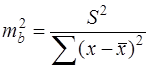
Таким образом, при 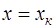получаем:

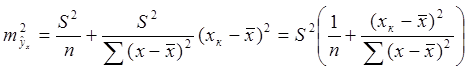
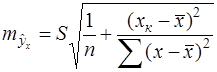(31)

Как видно из формулы, величина 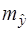достигает минимума при 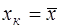и возрастает по мере удаления 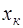от 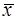в любом направлении.

Для нашего примера эта величина составит: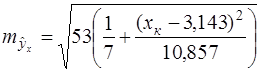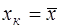

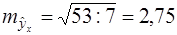При . При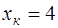

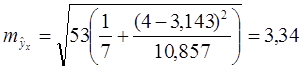
Для прогнозируемого значения 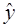95% - ные доверительные интервалы при заданном 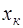определены выражением:

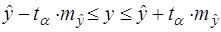(32)

то есть пр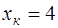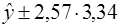и ил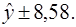и При 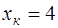прогнозное значение составит 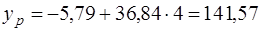- это точечный прогноз.

Прогноз линии регрессии лежит в интервале:

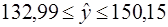
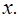Мы рассмотрели доверительные интервалы для среднего значения при заданном Однако фактические значения 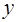варьируются около среднего значения 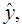они могут отклоняться на величину случайной ошибки ε, дисперсия которой оценивается как остаточная дисперсия на одну степень свободы 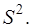Поэтому ошибка прогноза отдельного значения 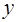должна включать не только стандартную ошибку 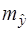, но и случайную ошибку S. Таким образом, средняя ошибка прогноза индивидуального значения 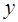составит:

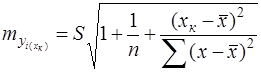(33)

где .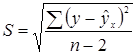

Для примера:

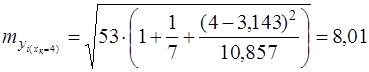
Доверительный интервал прогноза индивидуальных значени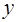й при 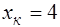с верностью 0,95 составит: 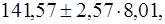или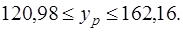

Пусть в примере с функцией издержек выдвигается предположение, что в предстоящем году в связи со стабилизацией экономики затраты на производство 8 тыс. ед. продукции не превысят 250 млн. руб. Означает ли это изменение найденной закономерности или затраты соответствуют регрессионной модели?

Точечный прогноз: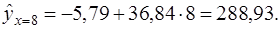

Предполагаемое значение - 250. Средняя ошибка прогнозного индивидуального значения:

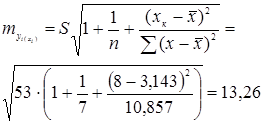
Сравним ее с предполагаемым снижением издержек производства, то есть 250–288,93=–38,93:

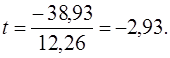
Поскольку оценивается только значимость уменьшения затрат, то используется односторонний t- критерий Стьюдента. При ошибке в 5 % с 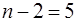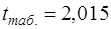, поэтому предполагаемое уменьшение затрат значимо отличается от прогнозируемого значения при 95 % - ном уровне доверия. Однако, если увеличить вероятность до 99%, при ошибке 1 % фактическое значение t – критерия оказывается ниже табличного 3,365, и различие в затратах статистически не значимо, то есть затраты соответствуют предложенной регрессионной модели.