Оценка параметров линейной регрессии
Линейная регрессия сводится к нахождению уравнения вида
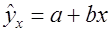 (или (или 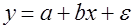 ) )
| (3) |
Первое выражение позволяет по заданным значениям фактора x рассчитать теоретические значения результативного признака, подставляя в него фактические значения фактора x. На графике теоретические значения лежат на прямой, которая представляют собой линию регрессии.
Построение линейной регрессии сводится к оценке ее параметров- а и b. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).
МНК позволяет получить такие оценки параметров а и b, при которых сумма квадратов отклонений фактических значений 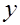 от теоретических
от теоретических 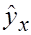 минимальна:
минимальна:
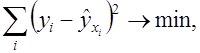 или или 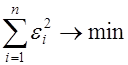
| (4) |
Для нахождения минимума надо вычислить частные производные суммы (4) по каждому из параметров - а и b - и приравнять их к нулю.
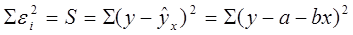
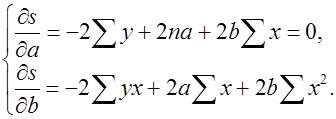 (5)
(5)
Преобразуем, получаем систему нормальных уравнений:
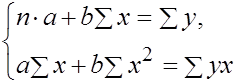 (6)
(6)
В этой системе n- объем выборки, суммы легко рассчитываются из исходных данных. Решаем систему относительно а и b, получаем:
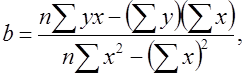 (7)
(7)
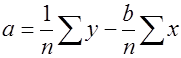 . (8)
. (8)
Выражение (7) можно записать в другом виде:
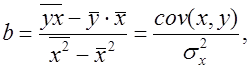 (9)
(9)
где 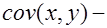 ковариация признаков,
ковариация признаков, 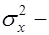 дисперсия фактора x.
дисперсия фактора x.
Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу.
Формально a- значение y при x=0. Если x не имеет или не может иметь нулевого значения, то такая трактовка свободного члена a не имеет смысла. Параметр a может не иметь экономического содержания. Интерпретировать можно лишь знак при параметре a. Если a> 0, то относительное изменение результата происходит медленнее, чем изменение фактора.
Рассмотрим в качестве примера по группе предприятий, выпускающих один вид продукции, регрессионную зависимость издержек от выпуска продукции 
Таблица 1
Выпуск продукции тыс.ед.( 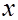 ) )
| Затраты на
производство, млн.руб.( 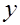 ) )
| 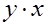
| 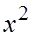
| 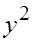
| 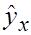
|
| 31,1 | |||||
| 67,9 | |||||
| 141,6 | |||||
| 104,7 | |||||
| 178,4 | |||||
| 104,7 | |||||
| 141,6 | |||||
| Итого: 22 | 770,0 |
Система нормальных уравнений будет иметь вид:
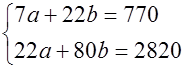
Решая её, получаем a= -5,79, b=36,84.
Уравнение регрессии имеет вид:
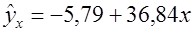
Подставив в уравнение значения х, найдем теоретические значения y (последняя колонка таблицы).
При линейной регрессии в качестве показателя тесноты связи выступает линейный коэффициент корреляции r:
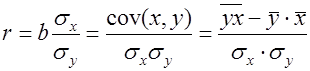
| (11) |
Его значения находятся в границах: 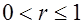 . Если b > 0, то
. Если b > 0, то 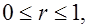 при b< 0
при b< 0 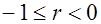 . По данным примера
. По данным примера 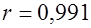 , что означает очень тесную зависимость затрат на производство от величины объема выпускаемой продукции.
, что означает очень тесную зависимость затрат на производство от величины объема выпускаемой продукции.
Для оценки качества подбора линейной функции рассчитывается коэффициент детерминации как квадрат линейного коэффициента корреляции r2. Он характеризует долю дисперсии результативного признака y, объясняемую регрессией, в общей дисперсии результативного признака:
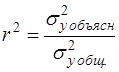
| (12) |
Величина 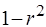 характеризует долю дисперсии y, вызванную влиянием остальных, не учтенных в модели факторов.
характеризует долю дисперсии y, вызванную влиянием остальных, не учтенных в модели факторов.
В примере 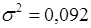 . Уравнением регрессии объясняется 98,2 % дисперсии
. Уравнением регрессии объясняется 98,2 % дисперсии 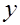 , а на прочие факторы приходится 1,8 %, это остаточная дисперсия.
, а на прочие факторы приходится 1,8 %, это остаточная дисперсия.
Дата добавления: 2016-07-27; просмотров: 2455;











