Доверительные интервалы для оценки среднего квадратического отклонения s нормального распределения

Пусть исследуемая случайная величина X генеральной совокупности распределена по закону N (a,s). По статистическим данным найдено “исправленное” среднее квадратическое отклонение S. Требуется найти для него доверительный интервал с надежностью g.

Требуется найти такое e > 0, чтобы выполнялось равенство

.

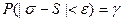Неравенство |s-S|<e с помощью ряда равносильных преобразований можно переписать в виде

.

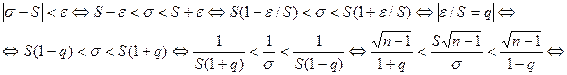
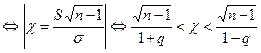Поэтому равенство (5.3.14) можно переписать в виде

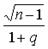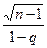P (|s-S|<e)=P ( <c< ) = g,

где

.

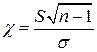Случайная величина распределена по закону 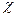(имеет 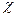- распределение) с 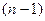степенями свободы. Плотность вероятности c-распределения с (n-1) степенями свободы имеет вид

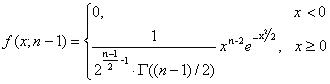
Тогда равенство (5.3.13) можно переписать в виде 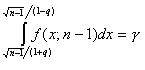. Из этого уравнения по заданным 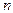и 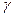можно найти 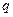; для этого используется табл. 6 вероятности попадания случайной величины с 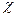- распределением в заданный интервал, зависящий от 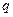. После нахождения 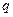доверительный интервал определяется равенством

.

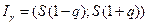Задача 5.3.4. Количественный признак генеральной совокупности распределен по нормальному закону N (a,s). По выборке объема 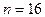найдено “исправленное” среднее квадратическое отклонение 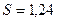. Найти доверительный интервал для этой оценки с надежностью .

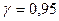Решение. По табл. 6 приложения по 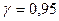и 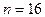найдем 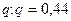. Доверительный интервал имеет вид I_g = (1,24(1–0,44); 1,24(1+0,44)) = (0,69;1,79).

Замечание. В теории измерений принято точность измерений (точность измерительной системы) характеризовать с помощью s. Для оценки s используют “исправленное” среднее квадратическое отклонение . Поэтому для оценки точности измерений применяется доверительный интервал для , теория построения которого изложена выше.