Градиентные стекловолокна как способ понижения межмодовой дисперсии

Назовем луч АС, распространяющейся вдоль оси симметрии волокна, центральным и обозначим отрезок АС = l_C (в соответствии с рисунком 3.15). Для луча АС АПП = n_C. Для луча АВ длина траектории l > l_C, а среднее значение АПП = n < n_C.

Скорость распространения луча АС V_C=С/n_C. Среднее значение скорости света, вдоль АВ = l, 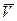= С/n. Поскольку n_C > n, V_C < 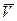. Время распространения света по траектории АС t_C = l_C /V_C. Время распространения света по траектории АВ t = l / .

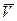Поскольку выполняется система неравенств l_C < l, V_C < 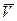, подбором профиля распределения АПП n(х), в соответствии с рисунком 3.17, можно добиться выполнения равенства t_C = t, и свести к минимуму межмодовую дисперсию t_MM, определяемую формулой (3.24).

Следует, однако, заметить, что приведенное в разделах 3.9 ¸ 3.11 рассуждение справедливы лишь для «прямых» лучей, распространяющихся в плоскости ABCD, проходящей через ось симметрии волокна и его диаметр (в соответствии с рисунком 3.16).

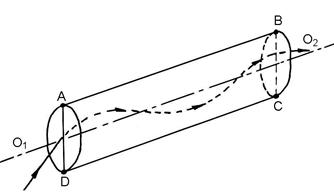
Рисунок 3.16 – Траектория «прямого» луча

Для «косых» лучей, не лежащих в вышеуказанной плоскости, траектория представляет собой винтовую линию (в соответствии с рисунком 3.17). Это значительно увеличивает длину траектории l и равенство t_C = t перестает выполнятся, а величина t_ММ начинает возрастать.

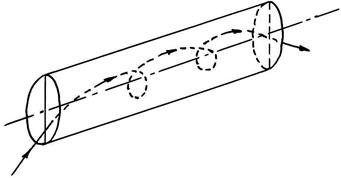
Рисунок 3.17 – Траектория «косого» луча

Формы распределения профиля абсолютного показателя преломления в стекловолокнах: форма распределения профиля АПП в градиентных СВ достаточно хорошо может быть представлена формулой общего вида

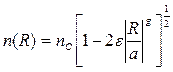(3. 39)

где R – радиус СВ;

n_C – АПП на оси симметрии СВ;

e = A²/2n 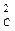, а – радиус центральной части СВ;

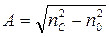– номинальная числовая апертура СВ;

n₀ – АПП оболочки СВ.

Согласно (2.39), при R = 0, n(R) = n_C. При 0 < R < a значения n(R) определяются коэффициентом g, который задает форму профиля АПП.

Параболический профиль: одним из самых распространенных профилей в современных СВ является параболический, для которого g = 2.

Такой профиль показан на рисунке 3.18 и, согласно (3.39), ему соответствует формула

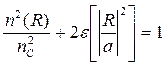(3.40)

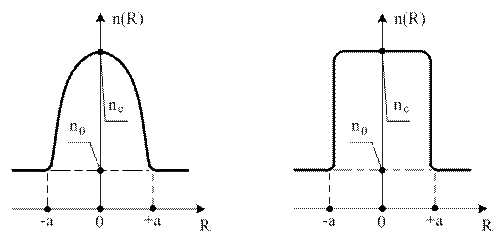
Рисунок 3.18 – Параболический Рисунок 3.19 – Ступенчатый

профиль распределения АПП профиль распределения АПП

в СВ в СВ

При R = 0, n(R) = n_C. На границе «центр-оболочка» R = a и, согласно (3.39) и (3.40), имеем

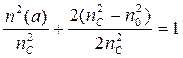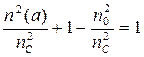, , n(a) = n₀. (3.40)