Градиент функции, его свойства.

Определение 8.3.

Вектор с началом в точке Р₀ и координатами 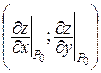называется градиентом функции z = f(x, y) в точке Р₀ и обозначается .

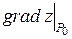Аналогично, градиентом функции и = f(x, y, z) в точке Р₀ называется вектор с началом в этой точке и координатами 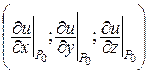, обозначается также .

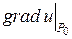Перечислим свойства градиента функции :

1) Производная функции и по направлению вектора 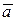равна проекции градиента этой функции на вектор 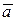, т.е. .

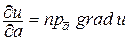Действительно

=

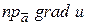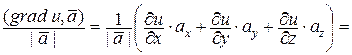
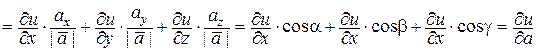
2) Производная по направлению принимает наибольшее значение, когда это направление совпадает с направлением градиента этой функции, т.е. 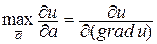. При этом .

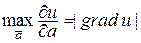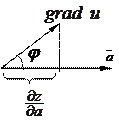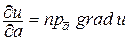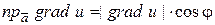Докажем это. Так как , а , где j – угол между вектором `а и .

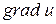Очевидно, это произведение принимает наибольшее значение, когда cosj = 1, т.е. j = 0, и, следовательно, направление 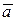совпадает с направлением 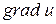. При этом наибольшее значение проекции, т.е. 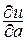, равно | 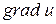|, ч.т.д.

Таким образом, градиент функции в точке Р₀ характеризует направление наискорейшего возрастания функции, а его модуль – величину наибольшей скорости роста функции при переходе через точку Р₀. При этом направление, противоположное направлению градиента, очевидно, характеризует направление наискорейшего убывания функции при переходе через данную точку.

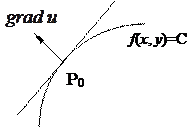3) Градиент функции в точке Р₀ перпендикулярен касательной, проведенной к линии (поверхности) уровня в этой точке.

Пример 2. Найти градиент функции 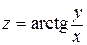в точке .

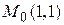В рассмотренном выше примере 1 найдено:

= ,

= .

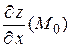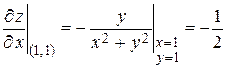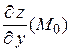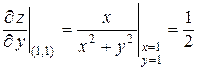Следовательно, градиент функции 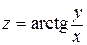в точке 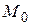равен

.

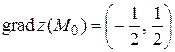Напомним, что градиент имеет простую физическую интерпретацию: этот вектор показывает направление, в котором при переходе через точку 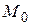данная функция растет быстрее, чем в любом другом направлении.