Расчет абсолютных и относительных показателей ряда динамики

Показатели ряда динамики могут быть:

• Абсолютные

• Абсолютные приросты

• Цепные

• Базисные

• Относительные

• Цепные

• Темпы (коэффициенты) роста

• Темпы (коэффициенты) прироста

• Абсолютное значение 1% прироста

• Базисные

• Темпы (коэффициенты) роста

• Темпы (коэффициенты) прироста

Абсолютный прирост характеризует размер увеличения (уменьшения) уровня ряда за определенный период времени и выражает абсолютную скорость роста, определяется по формуле:

DY_i-k = Y_i – Y_i-k, где i =1,2,3,4….,n, k=1,2,3,4….,m, (1)

где DY_i-k - абсолютный прирост уровня ряда,

Y_i- уровень ряда в году i,

Y_i-k - уровень ряда в году i- k,

Если к = 1, то уровень Y_k-1 является предыдущим для данного ряда , а абсолютные приросты будут цепными. Если же (i- к) постоянно для данного ряда (равно 0), то абсолютные приросты будут базисными (DY_i-k = Y_i – Y₀).

Коэффициент роста К_p или темп роста Т_p выражают интенсивность изменения уровня и рассчитывается по формуле:

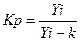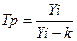или *100 % (2)

где Y_i-k =- уровень ряда в году i- k,_,

Коэффициент (темп) прироста K_пр (T_пр) характеризует относительную скорость изменения уровня ряда в единицу времени (за период) и определяется по формуле:

K_пр 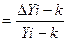, или K_пр = K_прi-к - 1,0,

T_пр 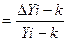*100 %, или T_пр = T_прi-к - 100 % (3)

Абсолютное значение одного процента прироста представляет собой одну сотую часть базисного уровня и рассчитывается по формуле:

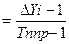/ %/ =0, 01 Yi-1 (4)