ПОСТРОЕНИЕ ВАРИАЦИОННЫХ РЯДОВ
Пусть из генеральной совокупности извлечена выборка, причем 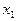 наблюдалось
наблюдалось 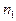 раз,
раз, 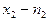 раз и т.д.,
раз и т.д., 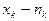 раз и
раз и 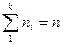 – объем выборки.
– объем выборки.
Наблюдаемые значения 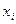 называются вариантами; последовательность вариант, записанных в порядке возрастания, называют вариационным рядом.
называются вариантами; последовательность вариант, записанных в порядке возрастания, называют вариационным рядом.
Числа наблюдений 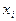 обозначены
обозначены 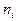 и называются частотами, а величины
и называются частотами, а величины 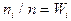 – относительными частотами. Статистическим распределением выборки называется перечень вариант
– относительными частотами. Статистическим распределением выборки называется перечень вариант 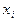 и соответствующих частот
и соответствующих частот 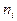 (или относительных частот
(или относительных частот 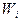 ):
):
| Х | 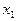
| 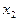
| ... | 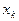
|
| nx | 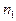
| 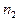
| ... | 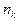
|
| Wx | 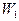
| 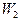
| ... | 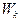
|
В случае большого количества вариантов и непрерывного распределения признака статистическое распределение выборки задают в виде последовательности интервалов и соответствующих им частот. Для этого интервал, в котором заключены все наблюдаемые значения признака, разбивают на определенное число частичных интервалов (x0, x1), (x1, x2),...,(xk-1, xk) длиной D хi и находят для каждого интервала ni сумму частот вариантов, попавших в i-й интервал. Таким образом получают интервальное статистическое распределение выборки:
| Интервалы | (x0, x1) | (x1, x2) | ... | (xk-1, xk) |
| nx | 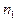
| 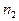
| ... | 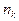
|
| Wx | 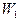
| 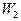
| ... | 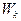
|
Статистическое распределение выборки называют также статистическим рядом.
Для графического изображения статистического ряда используют полигоны и гистограммы.
Для построения полигона на оси Ох откладывают значения вариант, на оси ординат – значения частот 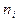 (или относительных частот
(или относительных частот 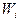 ). Построенную таким образом ломаную, отрезки которой соединяют точки (
). Построенную таким образом ломаную, отрезки которой соединяют точки ( 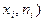 или
или 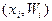 , называют полигоном частот или полигоном относительных частот соответственно.
, называют полигоном частот или полигоном относительных частот соответственно.
В случае непрерывного распределения признака на основании интервального статистического распределения используют гистограмму, устанавливающую зависимость частот от разрядов интервалов, в которые попадают значения случайной величины. Предполагаем, что длины интервалов равны 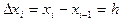 (h – шаг распределения). На оси Ox отметим точки
(h – шаг распределения). На оси Ox отметим точки 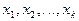 с шагом
с шагом 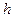 друг от друга. На каждом частичном интервале строим прямоугольник высотой
друг от друга. На каждом частичном интервале строим прямоугольник высотой 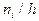 (плотность частоты). Гистограммой частот называют ступенчатую фигуру, состоящую из вышеупомянутых прямоугольников. Поскольку площадь i-го частичного прямоугольника равна
(плотность частоты). Гистограммой частот называют ступенчатую фигуру, состоящую из вышеупомянутых прямоугольников. Поскольку площадь i-го частичного прямоугольника равна 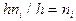 , то площадь гистограммы частот равна сумме всех частот, т.е. объему выборки n.
, то площадь гистограммы частот равна сумме всех частот, т.е. объему выборки n.
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению 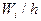 (плотность относительной частоты). Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят прямоугольники высотой
(плотность относительной частоты). Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят прямоугольники высотой  . Площадь i-го прямоугольника равна
. Площадь i-го прямоугольника равна 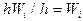 – относительной частоте вариант, попавших в i-й интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице. Поэтому гистограмма относительных частот является статистическим аналогом плотности распределения случайной величины X.
– относительной частоте вариант, попавших в i-й интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице. Поэтому гистограмма относительных частот является статистическим аналогом плотности распределения случайной величины X.
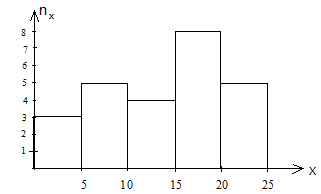
Задача В результате испытаний случайной величины X получен статистический ряд:
| I | 0-5 | 5-10 | 10-15 | 15-20 | 20-25 |
| nx |
Построить гистограмму частот и гистограмму относительных частот статистического ряда.
Решение. На рис. показана гистограмма частот
Построим статистический ряд относительных частот
| I | 0-5 | 5-10 | 10-15 | 15-20 | 20-25 |
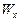
| 0,12 | 0,2 | 0,16 | 0,32 | 0,2 |
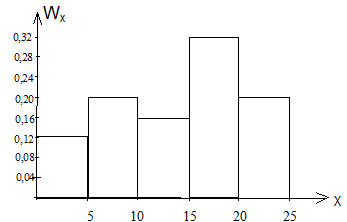
Пусть теперь изучается случайная величина X, закон распределения которой неизвестен. Требуется определить закон распределения на основании статистических данных.
Определение Статистической (эмпирической) функцией распределения (иначе функцией распределения выборки) называют функцию 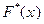 , определяющую для каждого значения х относительную частоту события
, определяющую для каждого значения х относительную частоту события 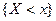 :
:
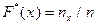 ,
,
где 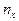 – число наблюдений, при которых значение признака X меньше x; n – объем выборки.
– число наблюдений, при которых значение признака X меньше x; n – объем выборки.
В отличие от эмпирической функции распределения 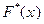 выборки функция распределения
выборки функция распределения 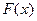 генеральной совокупности называется теоретической функцией распределения. Различие между эмпирической
генеральной совокупности называется теоретической функцией распределения. Различие между эмпирической 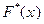 и теоретической
и теоретической 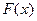 функциями распределения состоит в том, что
функциями распределения состоит в том, что 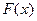 определяет вероятность события
определяет вероятность события 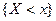 , а
, а 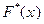 - относительную частоту этого же события. Поэтому
- относительную частоту этого же события. Поэтому 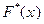 можно использовать для приближенного представления теоретической функции распределения генеральной совокупности.
можно использовать для приближенного представления теоретической функции распределения генеральной совокупности.
Функция 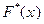 обладает свойствами
обладает свойствами 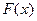 :
:
1) значения эмпирической функции распределения принадлежат отрезку [0,1];
2) 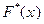 является неубывающей функцией на промежутке
является неубывающей функцией на промежутке 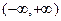 ;
;
3) если 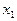 – наименьшая варианта, то
– наименьшая варианта, то 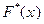 = 0 при
= 0 при 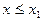 ;
;
если 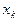 – наибольшая варианта, то
– наибольшая варианта, то 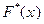 = 1 при
= 1 при 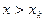 .
.
Задача 2. Построить эмпирическую функцию распределения по статистическому распределению
| X | ||||
| Wx | 0,4 | 0,1 | 0,3 | 0,2 |
Решение. Имеем
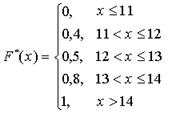 .
.
Дата добавления: 2016-07-27; просмотров: 2481;











