Активная, реактивная, полная мощность

Мгновенная мощность цепи с RL и С элементами

В общем случае мгновенная мощность определяется произведением тока на напряжение:

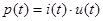. (4.1)

Определим мгновенную мощность для цепи с последовательно включенными R, L и С элементами (рис.3.1). Пусть в этой цепи протекает ток

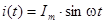. (4.2)

Он одинаков для всех элементов цепи.

Напряжение цепи определяется суммой падений напряжений на отдельных элементах

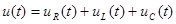. (4.3)

С учетом выражений (1.8) и (1.11) перепишем (4.3):

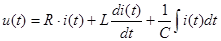. (4.4)

Подставляя в (4.4) выражение для i(t) и, решая его, получим

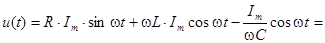
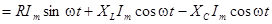. (4.5)

Теперь, подставляя (4.2) и (4.5) в (4.1) находим выражение для мгновенной мощности цепи рис. 3.1:

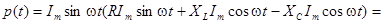
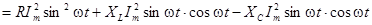. (4.6)

Выражение (4.6) показывает, что мгновенная мощность цепи определяется суммой слагаемых мощностей каждого из элементов. Это требует более детального анализа (4.6).

Активная, реактивная, полная мощность

Для анализа (4.6) применим известные из курса тригонометрии формулы преобразования:

.

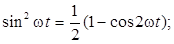
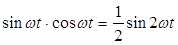Применяя их к (4.6) получим:

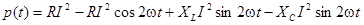, (4.7)

где I - действующее значение тока, причем .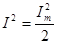

Первые два слагаемых в (4.7) определяют мгновенную мощность, выделяемую на элементе R. Можно записать, что:

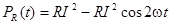. (4.8)

Как видно из (4.8) мгновенная мощность p_R(t) содержит постоянную составляющую Р = RI² и переменную, меняющуюся с удвоенной частотой. График р_R(t) приведен на рис. 4.1. График наглядно показывает, что мощность р_R(t) всегда положительна и изменяется от 0 ( в момент t=0, k×T/2) до 2RI² ( в моменты (2k-1)× T/4), Т=2p/w - период тока.

Среднее за период значение мощности обозначают Р и называют активной мощностью, причем:

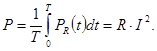(4.9)

Для более детального анализа мгновенной мощности Р_R(t) обратимся к выражению (4.5). Этому выражению соответствует векторная диаграмма рис.4.2. В ней в качестве исходного принят вектор тока 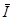. Вектор напряжения на индуктивности 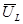опережает ток, а на емкости 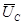отстает от тока на 90^о. Напряжение на резисторе 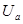совпадает по фазе с током.

Проведем сложение векторов. Для этого начало вектора 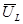переместим в точку конца вектора 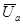, а начало вектора 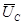- в точку конца вектора 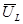. Результатом сложения является вектор 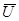выходящий из начала вектора 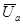в конец вектора 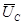. Угол j определяет сдвиг фаз между током и результирующим напряжением, т.е.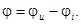

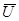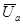Соединим точки концов двух векторов - и . Обозначим вновь полученный вектор 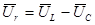. Образовавшийся треугольник из векторов 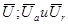называют треугольником напряжений. Для него справедливы следующие выражения:

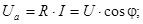
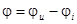(4.10)

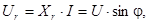
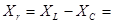
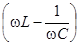(4.11)

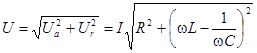(4.12)

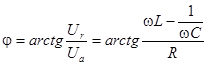(4.13)

Возвратимся вновь к анализу мгновенной мощности, выделяемой на элементе R - p_R(t). С учетом (4.10) перепишем (4.8) в виде

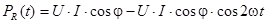(4.14)

Первое слагаемое в правой части полностью соответствует (4.9) т.е. определяет активную мощность

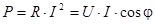[Вт] (4.15)

Выражение (4.15) используется в практике намного чаще, так как определяет зависимость активной мощности от сдвига фаз между действующими значениями тока и напряжения цепи. В силу этого коэффициент cos j называют коэффициентом мощности и обозначают l

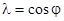. (4.16)

Обратимся к исходному выражению для мгновенной мощности цепи - (4.7). В нем третье и четвертое слагаемые определяют мощность, выделяемую на реактивных элементах – индуктивности

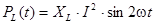(4.17)

и емкости

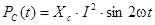(4.18)

Каждое из этих слагаемых изменяются с удвоенной (относительно тока) частотой, но имеют противоположные фазы (рис.4.3). Так как постоянная составляющая в (4.17) и (4.18) отсутствует, то среднее значение каждого из них равно нулю. Однако сумма p_L(t) и p_C(t) отлична от нуля и определяет мгновенную мощность реактивных элементов (участков) цепи. Определим ее:

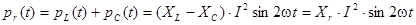(4.19)