Вынужденные колебания в линейной системе при гармоническом воздействии
Для линейных стационарных систем выполняется принцип суперпозиции: если воздействие x1(t) порождает реакцию u1(t), а воздействие x2(t) реакцию u2(t), тогда воздействие, которое является линейной комбинацией первых двух a1x1(t) + a2x2(t) порождает следующую реакцию a1u1(t) + a2u2(t). Этот принцип означает, что в таких системах отсутствует нелинейное взаимодействие колебаний, вызванных различными одновременными действующими внешними силами. Будем считать, что собственные колебания в диссипативной системе достаточно быстро затухают, и можно анализировать только вынужденные колебания, т. е. рассматривать установившийся режим
Рассмотрим простейший RLC контур с источником гармонического воздействия u1(t) с частотой w1 (рис. 26), тогда колебательный процесс будет описываться линейным ДУ:
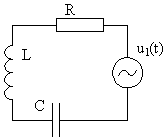 Рис. 26. Колебательный контур с вынуждающей силой
Рис. 26. Колебательный контур с вынуждающей силой
| 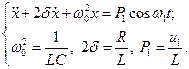
| (4.1) |
Решением неоднородного ДУ (4.1) является сумма решений однородного уравнения, т. е. собственных колебаний, и частного решения неоднородного уравнения, т. е. вынужденных колебаний. Собственные колебания описываются уравнением (3.23)
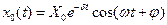 , где , где 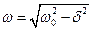 . .
|
Начальную фазу надо отсчитывать от внешнего воздействия. При гармоническом воздействии внешней силы реакция линейной системы есть гармонический сигнал:
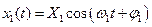 .
.
Подставим это выражение в (4.1):
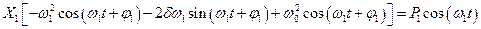 .
.
Воспользовавшись равенством
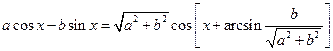 ,
,
преобразуем получившееся уравнение к виду
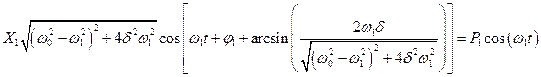 .
.
Приравнивая амплитуды и фазы в правой и левой частях этого уравнения, получим
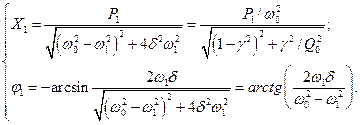
| (4.2) |
Мы обозначили g = w1/w0 - расстройка, Q0 = w0L/R - добротность. Из (4.2) следует, что j1(w1 ® 0) = 0, j1(w1 = w0) = p/2, j1(w1 ® ¥) = p.
Решим эту задачу методом комплексных амплитуд. Сопоставим току и напряжению их комплексные амплитуды, а также вспомним реактивные сопротивления, тогда можно записать
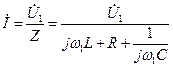 .
.
Найдём модуль
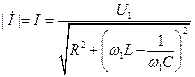 .
.
Нетрудно видеть, что максимальное значение тока:
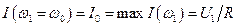 .
.
Введём форм-фактор, который определяет семейство нормированных резонансных кривых (в данном случае для тока)
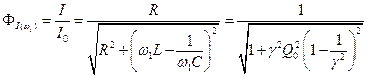 .
.
График этой функции приведён на рис. 27. Напряжение на резисторе пропорционально току через контур uR = iR, т. е. амплитуда напряжения на резисторе достигает максимума при w1 = w0. Зависимость фазы напряжения на резисторе от расстройки приведена на рис. 28.
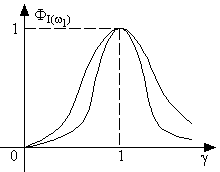 Рис. 27. Семейство нормированных резонансных кривых для разных значений добротности Q0.
Рис. 27. Семейство нормированных резонансных кривых для разных значений добротности Q0.
| 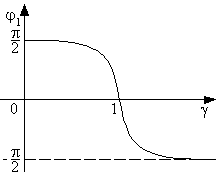 Рис. 28. Зависимость фазы напряжения на сопротивлении R от расстройки.
Рис. 28. Зависимость фазы напряжения на сопротивлении R от расстройки.
|
Исходя из операций с комплексными амплитудами, легко получить выражения для напряжений на всех элементах рассматриваемого колебательного контура. Для комплексной амплитуды напряжения на конденсаторе получаем
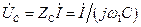 .
.
Соответственно, фаза напряжения на конденсаторе сдвинута относительно фазы напряжения на резисторе на -p/2. Резонанс напряжения на ёмкости 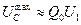 получается при
получается при 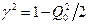 , т. е. при более низкой, чем w0 частоте w1.
, т. е. при более низкой, чем w0 частоте w1.
Для комплексной амплитуды напряжения на индуктивности получаем
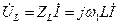 .
.
Фаза напряжения на индуктивности сдвинута относительно фазы напряжения на резисторе на p/2. Резонанс напряжения на индуктивности 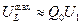 достигается при
достигается при 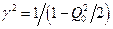 , т. е. на более высокой, чем w0 частоте w1. Нужно отметить, что для достаточно высокой добротности контура эта разница частот резонанса напряжений на резисторе, конденсаторе и индуктивности несущественна. Все три максимума совпадают только при Q0 ® ¥.
, т. е. на более высокой, чем w0 частоте w1. Нужно отметить, что для достаточно высокой добротности контура эта разница частот резонанса напряжений на резисторе, конденсаторе и индуктивности несущественна. Все три максимума совпадают только при Q0 ® ¥.
Дата добавления: 2019-02-08; просмотров: 970;











