Линейный контур с затуханием
| Рассматриваем RLC колебательный контур - простейшая система с затуханием. Мы зарядили конденсатор, и в момент времени t0 замкнули ключ (рис. 22). Уравнение колебаний в такой системе: | 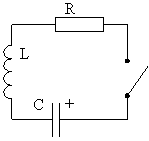 Рис. 22. Линейный контур с затуханием.
Рис. 22. Линейный контур с затуханием.
| |
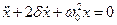 , где , где 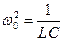 , , 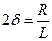 . .
| (3.2) | |
Точка равновесия x = 0 представляет собой устойчивый фокус.
Найдём уравнение фазовых траекторий. Для этого преобразуем это уравнение стандартным образом:
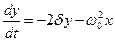 , , 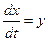 . .
| ||
Откуда просто получаем уравнение фазовых траекторий
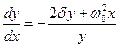 . .
| (3.3) |
Это уравнение не очень удобно, так как в правой части зависит как от x, так и от y, поэтому введём новую переменную z = y/x, тогда (3.3) перепишем в виде
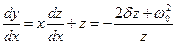 .
.
Выполним некоторые элементарные преобразования:
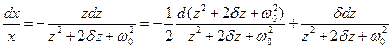 ,
,
или, проинтегрировав,
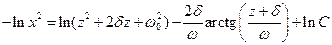 ;
;
мы обозначили 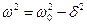 . Запишем z через x и y, и возведём в exp:
. Запишем z через x и y, и возведём в exp:
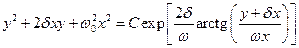 . .
| (3.4) |
У нас получились уравнение фазовой траектории в явном виде. Придадим этому уравнению более удобную форму. Для этого введём ещё одни новые переменные u = y + dx, v = wx. Если w0 > d (затухание мало), то w действительное число, тогда (3.4) принимает вид:
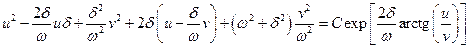 .
.
Перейдём к полярным координатам: v = rcosj, u = rsinj, тогда
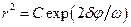 . .
| (3.5) |
Интегральная кривая соответствующая этому случаю изображена на рис. 23.
Если затухание велико, т. е. w0 < d, тогда w2 отрицательное, и w - мнимое число (w = iq). Опять, путём несложных преобразований, получим уравнение
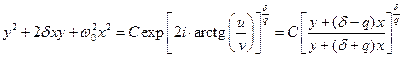 . .
| (3.6) |
Фазовый портрет для этого случая показан на рис. 24.
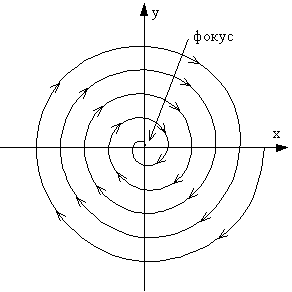 Рис. 23. Фазовый портрет системы с затуханием меньше критического.
Рис. 23. Фазовый портрет системы с затуханием меньше критического.
| 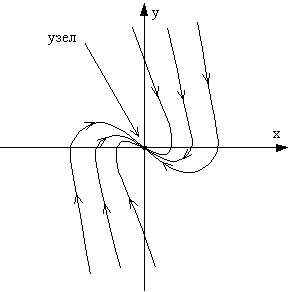 Рис. 24. Фазовый портрет системы с затуханием больше критического.
Рис. 24. Фазовый портрет системы с затуханием больше критического.
|
При w0 > d мы имеем дело с затухающими колебаниями линейного осциллятора, фазовый портрет которых представляет собой совокупность спиралей, стягивающихся в особую точку типа фокус. Для w0 < d система становится апериодической, и на фазовой плоскости движения изображаются фазовыми траекториями, имеющими вид кривых, сходящихся в особую точку типа узел без обхода вокруг неё. В обоих случаях в диссипативных системах особые точки (фокус и узел) устойчивы и соответствуют единственному положению равновесия системы - состоянию покоя, к которому система приходит из любых начальных условий, при любом начальном смещении или скорости.
Дата добавления: 2019-02-08; просмотров: 861;











