Метод медленно меняющихся амплитуд, укороченные уравнения

Вопрос 7

Метод медленно меняющихся амплитуд (ММА) применим к системам с малыми нелинейностью и диссипацией и основан на известной теореме, что свойства системы и решение описывающего её ДУ изменяются непрерывно при изменении параметров этого уравнения. При малых нелинейностях и диссипации движение в системе будет близко к чисто гармоническому, соответствующему линейной консервативной системе, уравнение которой имеет вид

.

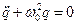Введём безразмерное время t = w₀t, тогда в этом масштабе времени уравнение будет таким

.

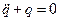Для системы близкой к линейной консервативной уравнение выглядит так:

,

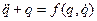(3.7)

где f - произвольная регулярная, в общем случае нелинейная функция координаты q и скорости её изменения, значения которой остаются малыми по сравнению со значениями членов, стоящих в левой части уравнения (3.7) (в силу слабой нелинейности параметров и малых потерь в системе).

Выберем в уравнении (3.7) масштаб по координате q и перейдём к безразмерной переменной x так, чтобы при колебаниях изменение x было порядка единицы, тогда правая часть (3.7) должна быть много меньше единицы:

,  .

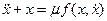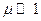(3.8)

При m = 0 решением уравнения будут чисто гармонические колебания

,

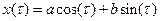где a и b - постоянные, задаваемые начальными условиями.

При 0 < |m| < 1 будем считать, что решение может быть записано в виде

,

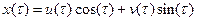(3.9)

где u(t) и v(t) - медленно меняющиеся функции (в сравнении с cos(t)), так что

, .

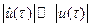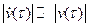Но получается, что одной функции x(t) ставятся в соответствие две функции u(t) и v(t), т. е. задача становится заведомо неоднозначной. Можно произвольно задать одну из функций и подобрать к ней вторую, при этом, если мы не угадаем, то эта функция будет быстро меняться. Потребуем, чтобы функция x(t) удовлетворяла условию:



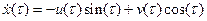
(3.10)

для чего необходимо и достаточно, чтобы



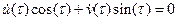
(3.11)

При выполнении условия (3.11) уравнение-связь (3.9) становится однозначным, т. е. становится однозначной связь функций x(t), u(t) и v(t).

Используя уравнения (3.9) - (3.11), преобразуем (3.8): продифференцируем (3.10) по времени и сложим с (3.9) с учётом (3.8):

.

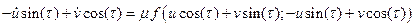(3.12)

Умножим (3.12) на sin(t), а (3.11) на cos(t) и вычтем из первого второе; потом умножим (3.12) на cos(t), а (3.11) на sin(t) и сложим их, тогда получим систему:

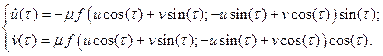
(3.13)

Таким образом, мы получили систему двух уравнений первого порядка (3.13), которая, естественно, полностью эквивалентна одному уравнению второго порядка (3.8). Она не даёт никаких преимуществ в смысле упрощения задачи. Существенный в шаг в сторону нахождения приближенного решения можно сделать, если воспользоваться условием медленного изменения функций u и v за период. Заменим мгновенные значение u и v их средними значениями за каждый период колебаний, равный 2p. Производя усреднение по периоду, мы приходим к системе так называемых укороченных уравнений

;

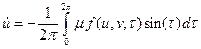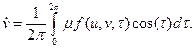
(3.14)

Эта система уже не содержит в правой части в явном виде времени t, и во многих случаях её можно легко проинтегрировать, получая временной ход медленно меняющихся функций u(t) и v(t), являющихся амплитудами искомого решения.

Систему уравнений (3.14) можно получить из системы (3.13), если правые

части разложить в ряд Фурье как периодические функции с периодом 2p и отбросить все осциллирующие члены (в системе (3.14) записаны только первые слагаемые ряда). В этом отбрасывании осциллирующих членов и заключается "укорочение", приводящее от системы уравнений, точно соответствующей исходному уравнению, к приближенным укороченным уравнениям.

Переход от переменных x, 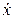к переменным u, v эквивалентен переходу от фазовых координат x, 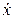к вращающейся системе координат u, v. Это означает, что система координат u, v в координатной плоскости x, 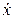вращается с угловой частотой, равной единице.

Рассмотрим теперь другой вариант метода ММА с переходом от исходных координат x, 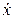к радиальным координатам - амплитуде X и фазе q, которые также являются медленными переменными в масштабе времени t.

Будем теперь искать решение исходного уравнения (3.8) в виде

.

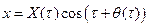(3.15)

Введём замену переменной :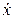

,

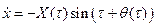(3.16)

для чего необходимо положить

.

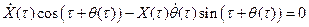(3.17)

Дальше дифференцируем (3.16) по времени, с учётом равенства (3.17), и вместе с (3.15) подставляем в исходное уравнение (3.8), тем самым, выражая его через новые переменные X и q.

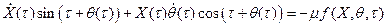
(3.18)

Из (3.17) и (3.18) находим точную систему дифференциальных уравнений, описывающих процессы в системе

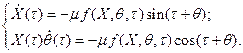
(3.19)

Здесь X(t) и q(t) являются медленными функциями времени t, что позволяет усреднить правые части (3.19) за период, считая, что за это время X и q не меняются. Указанная процедура усреднения приводит к системе укороченных уравнений вида

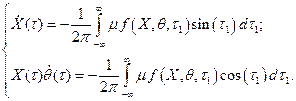
(3.20)

Мы обозначили t₁ = t + q.

Найдём спектр ММА колебания. Для этого запишем сигнал ММА (3.15) в реальном масштабе времени:

.

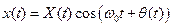Предполагается, что соотношение (3.16) выполняется, а центральная частота w₀ выбирается так, чтобы амплитуда колебаний X(t) менялась как можно медленнее. Условие медленного изменения амплитуды принимает вид:

,  .

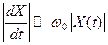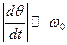(3.21)

Спектр ММА процесса будет

.

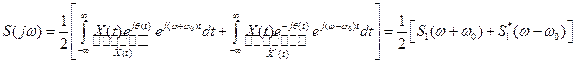Здесь мы обозначили спектр комплексной огибающей колебания :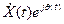

.

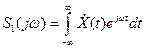У нас и X, и q меняются медленно, тогда комплексная огибающая меняется медленно по сравнению с характерным временем 1/w₀. Это значит, что t >> 1/w₀, где t - характерное время изменения комплексной огибающей.

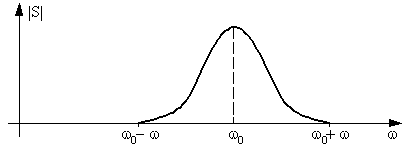Рис. 25. Спектр сигнала.

Можно определить ширину спектра Dw из условия, что при |w - w0| > Dw спектр сигнала S(jw) º 0. В теории интегралов Фурье установлена связь между шириной полосы спектра и временем характерного изменения импульса: tDw ~ 1. Таким образом, любой узкополосный процесс, для которого

Dw << w₀, является ММА процессом, но обратное не обязательно.