Тема 3. Свободные колебания в диссипативных системах с одной степенью свободы Вопрос 6

В неконсервативных системах полная энергия не сохраняется, поэтому уравнение фазовых траекторий уже не может иметь вид уравнения (2.5). Мы можем записать его с учётом соотношения (1.35), где введена функция Рэлея, которая описывает убыль энергии. Функция Рэлея:

; 

Так как функция F(x, y) описывает убыль энергии, то можно сказать, что функция W(t) определяет запас колебательной энергии системы. В консервативной системе она бы сохранялась. Естественно, что для автономных диссипативных систем dW/dt < 0, т. е. энергия с течением времени уменьшается.

Для простейшей диссипативной системы уравнение (2.5) принимает вид:

;  .

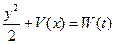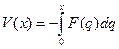(3.1)

Введём так называемую функцию диссипации

.

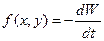Теперь продифференцируем уравнение (3.1) по времени, тогда

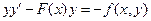или .

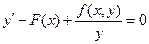Это уравнение по сути дела есть уравнение закона Ньютона: ускорение равняется действующей силе. Здесь F(x) - потенциальная сила, зависящая от координаты, а f(x, y)/y - сила трения, зависящая от скорости.

В физически реализуемых колебательных системах диссипация всегда связана с движением. Для покоящегося тела диссипации быть не должно, т. е. f(x, y)/y ® 0 при y ® 0. Мы сказали, что для диссипативных систем dW/dt < 0, а это значит, что функция f(x, y) > 0. Следовательно, функция f(x, y)/y имеет знак совпадающий со знаком y.

Наличие диссипации в системе изменяет характер особых точек. Если для математического маятника особыми точками были центр и седло, то для диссипативных систем вместо центра появляются фокус или узел, в зависимости от величины диссипации.

Для анализа систем с малыми диссипациями и малыми нелинейностями существуют специальные приближённые методы, в частности, метод медленно меняющихся амплитуд. Рассмотрим этот метод на задачах, имеющих аналитическое решение (чтобы было с чем сравнивать), а потом уже будем применять там, где нет аналитических решений.