В неориентированном графе понятие дуга, путь, контур заменяются соответственно на ребро, цепь, цикл.
Ребро — отрезок, соединяющий две вершины, цепь — последовательность ребер.
Цикл — конечная цепь, у которой начальная и конечная вершина совпадают.
Граф называется связанным, если любые его две вершины можно соединить цепью. Граф сильно связан, если для его двух любых вершин х. * х. существует путь, идущий из х(. и xf
Граф, который не является связанным, может быть разбит на конечное число связных графов, называемых компонентами, или частями.
Ребро графа G называется мостом, если граф, полученный из G путем удаления этого ребра, имеет больше компонент связности, чем граф G.
Точкой сочленения графа называется вершина, удаление которой приводит к увеличению числа его компонент связности.
На рисунке 3 ребро k — мост, а на рисунке 4 вершина 1 — точка сочленения.
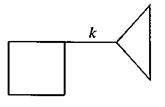
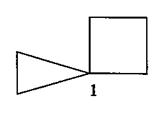
Рис. 3 Рис. 4
Неразделимым называется связный граф, не имеющий точек сочленения. Блоком графа называют максимальный неразделимый подграф.
На рисунке 5 приведен граф G и его блоки А, В, С и D.
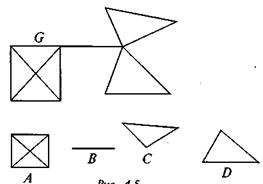
Рис. 5
Дерево это конечный, связный, не ориентированный граф, не имеющий циклов.
Характеристическое свойство деревьев состоит в том, что любые две вершины дерева соединены единственной цепью.
Теория деревьев была, в основном, разработана Кирхгофом. Он применил ее для решения систем линейных уравнений, описывающих работу электрических цепей.
Развитие теории графов (деревьев) связано с именем немецкого химика Кели, который успешно применил ее для решения задач органической химии (для изучения изомеров углеводородов с заданным числом атомов).
Совокупность деревьев называется лесом.
Если все вершины графа принадлежат дереву, то он называется покрывающим. Пусть дано множество вершин графа. Одну из вершин, например хр примем за начальную, которую назовем корнем дерева. Из этой вершины проводим ребра к остальным вершинам х2, х3 и т. д. Простейшее дерево состоит из двух вершин, соединенных ребром.
Если добавить ребро, то добавляется и вершина. Таким образом, дерево с п вершинами имеет п—1 ребро.
Дерево, являющееся подграфом графа G, называется покрывающим граф G, если оно содержит все его вершины.
Матрицей смежности S порядка п называется матрица, состоящая из чисел Sij, равных сумме чисел ориентированных ребер, идущих из хi в хj (или чисел неориентированных ребер, соединяющих эти вершины). Если дуга отсутствует, то Sij = 0.
Матрица смежности для ориентированного и неориентированного графа, вообще говоря, имеет разный вид. Запишем матрицу смежности S, для ориентированного графа, изображенного на рисунке 6:
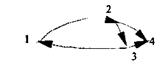
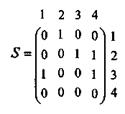
Рис. 6
Матрицей инциденции Т размера т х п называется матрица, состоящая из чисел:
|
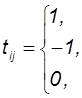
Запишем матрицу инциденции для графа, изображенного на рисунке 6:

Рассмотрим подробно решение задачи о Кенигсбергских мостах. В городе Кенигсберге имеется остров Кнайпхоф, который охвачен двумя рукавами реки Пречель. Через два рукава перекинуты семь мостов: а, Ь, с, d, e, f, g. Можно ли спланировать прогулку таким образом, чтобы по каждому мосту пройти только один раз и вернуться в начальное положение? Поставим в соответствие каждому мосту ребро графа, а суше вершину (рис. 7)
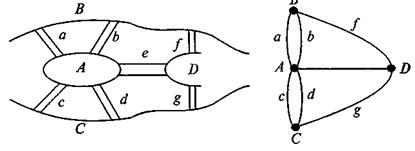
Рис. 7
Эйлеровым путем в графе G называется такой путь в котором каждое ребро встречается один раз. Эйлер доказал, что такой путь существует тогда и только тогда, когда граф G содержит не более двух вершин нечетной степени и являются связными. В данной задаче существует четыре вершины нечетной степени (5, 3, 3, 3). Таким образом, задача о Кенигсбергских мостах не содержит Эйлеров путь и не имеет решения.
Если граф содержит точно две вершины нечетной степени, то в эйлеровом пути эти вершины должны быть конечными.
Если вершин нечетной степени нет, то граф имеет замкнутый эйлеров путь.
На рисунке 8а нет замкнутого эйлерова пути; на рисунке 8б эйлеров путь замкнут.
|
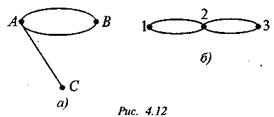
В XIX в. Гамильтон придумал игру, состоящую в том, что на доске располагались города в виде додекаэдра (рис. 9).
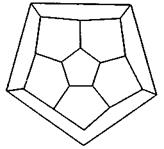
Рис. 9
Играющий (игрок) должен обозначить шнуром замкнутый круг, соединяющий последовательно одну вершину с другой, посетив при этом все города, зайдя в каждый только один раз. Граф G называют Гамильтоновым, если он содержит простейший путь, проходящий через его вершину.
Задача о коммивояжере принадлежит к классу задач математического программирования. Требуется найти такой путь коммивояжера, по которому необходимо посетить п—1 городов, зайдя в каждый город, вернуться домой, причем протяженность пути должна быть минимальной. Таким образом, среди всех гамильтоновых циклов графа с п вершинами нужно найти сумму длин ребер, путь по которым будет минимальным. Математически эта задача решения не имеет.
Дерево игры — это способ описания игры, в которой последовательно, по ходам, фиксируется, какой информацией должны располагать игроки, какие варианты они могут выбрать, а также средний размер платежей в конце игры. Игра, описываемая при помощи такого дерева, называется игрой в развернутой форме или позиционной игрой.
Дерево решений — это система, отражающая структуру оптимизации задачи принятия решений. Ветви — это события, которые имеют место, а вершины — состояния в которых возникает проблема выбора. Узлы выбора различны. В одних решения принимает руководитель, в других выбор производит «природа», т. е. выбор ситуации от руководителя не зависит и он может только оценить вероятность принятия того или иного решения. Дерево решений применяется тогда, когда количество альтернатив и принятых решений конечно.
Построение деревьев решений используют при решении задач динамического распределения памяти ЭВМ. В динамическом программировании решение задачи планирования работ называют проектом. Нужно выбрать наилучший проект за заданное время с использованием выделенных ресурсов. Существуют два способа математического решения этой задачи.
1) Метод кратчайшего пути.
2) Проект оценки и пересмотра проекта. Характерным для этих методов является изображение проекта в виде сети взаимосвязанных работ.
Контрольные вопросы.
1. Что такое граф? Пример
2. Какой граф называется ориентированным? Пример
3. Какой граф называется неориентированным? Пример
4. Что называется петлей? Пример
5. Какие вершины называются смежными? Пример
6. Какое ребро называется инцидентным? Пример
7. Что такое степень вершины? Пример
8. Что такое кратность пары вершин? Пример
9. Что такое подграф? Пример
10. Что такое частный граф? Пример
11. Что называется путем в графе? Пример
12. Что называется длиной пути в графе? Пример
13. Что такое дерево? Пример
14. В чем заключается задача о коммивояжере? Пример
15. Способы решения задачи о коммивояжере
16. Каким способом в дискретной математике решают задачу коммивояжере?
Лекция № 11
Тема: «Структуры и стратегии поиска с помощью графов»
План лекции
1. Оптимизация решений динамическими методами
2. Метод динамического планирования
3. Метод ветвей и границь.
1. Оптимизация решений динамическими методами
Одной из особенностей, свойственных проблемам принятия решения есть то, что они, как правило, являются сложными проблемами, которые плохо формализируются и трудно решаются. В силу этого решения таких проблем может осуществляться простым перебором всех возможных вариантов. Потом оценивают и сравнивают результаты разных вариантов решений и принимают лучший (оптимальный) вариант.
Методы решения, основанные на переборе получили название комбинаторных. Комбинаторный аспект заложен в каждой проблеме принятия решения, а решение любой проблемы состоит из выбора последовательности действий, наиболее приемлемой для заданной исходной ситуации.
В зависимости от избранной математической модели методы принятия решений разделяются на следующие три класса, которые принципиально отличаются подходами к проблеме:
1) комбинаторные, то есть основаны па организации поиска (перебору) решений;
2) аналитические, основанные на превращениях аналитических формул;
3) сетевые, основанные на построении потоков в сетях.
Хотя аналитические и сетевые методы довели свою эффективность при решении большой числа конкретных проблем, область их приложения очень ограничена. Значительно шире является область применения комбинаторных методов.
В экономике, организации, планировании и управлении производством часто встречаются случаи, когда цель оптимального решения задачи заключается в установлении наилучшей последовательности выполнения тех или других работ (производственных операций, состояний строительства разного рода сооружений и так далее).
Именно эта оптимальная последовательность работ или действий ведет к наилучшим результатам работы организации: максимальной прибыли, минимума временных и финансовых расходов, максимальной рентабельности работы. Определение цеп оптимальной последовательности происходит последовательно с помощью полного или частичного перебора возможных вариантов на базе ЭВМ. Машина генерирует возможный вариант решения, анализирует его и делает вывод о его перспективности (запоминая его) или не перспективности (отбрасывая его). В результате такой сортировки на каждом шагу выделяется все меньше и меньше приемлемых вариантов. Па окончания такого динамического анализа выделяется одно или несколько лучших решений.
Одной из первых задач такого рода, которая обратила внимание специалистов, была так называемая задача о коммивояжере.
Коммивояжер (агент, который рекламирует товар своей фирмы), повинный посетить (п-1) мост и вернуться в исходный пункт. Известны расстояния между городами. Нужно установить, в каком порядке коммивояжер должен посещать города, чтобы общая пройденная расстояние было минимально.
Задачу коммивояжера для наглядности удобно представить в виде графа или таблицы с указанием расстояний между пунктами. Количество маршрутов к=(п–1)!, где п – число пунктов (мост). Количество маршрутов очень быстро растет в меру увеличения числа п. Так, 4!=24; 5!=120; 10!=3628800 маршрутов. Оценить и сравнить такую массу маршрутов трудно даже с помощью ЭВМ. Отсюда выплывает необходимость поиска других методов, основанных па существовании гамильтоновых путей на графе.
Проблема заключается в том, чтобы резко сократить перебор вариантов, отбрасывая сознательно непригодные. Как же это сделать? Оказывается, можно - с помощью метода динамического планирования. Чтобы была понятна суть метода, рассмотрим следующий пример.
2. Метод динамического планирования
Фирма обеспечивает снабжение товаров для продажи из базы А0 в четыре торговых точки А1, А2, А3, А4. Расстояния между всеми пунктами известны и заданы в километрах (Таблица 1).
В целях экономии времени и средств необходимо найти такой маршрут передвижения, при котором, побывав в каждой торговой точке по одному разу, поставщик вернулся бы в начальный пункт А0, пройдя минимально возможный суммарный путь.
Таблица 1 – Начальные данные.
| А0 | А1 | А2 | А3 | А4 | |
| А0 | |||||
| А1 | |||||
| А2 | |||||
| А3 | |||||
| А4 |
Решение
Видно, что матрица симметрична относительно главной диагонали, потому достаточно информации одной из ее половин. Расстояния определяются для конкретных путей сообщения не обязательно по прямой. Для определения кратчайшего пути коммивояжера будем рассматривать варианты его передвижения последовательно, пункт за пунктом.
Начинаем с вариантов, которые состоят из трех участков. Например, отправляясь из начального пункта A0 можно добраться в третий пункт А3 шестью способами:
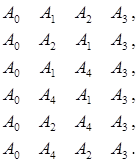
Зная расстояния между пунктами, можно вычислить суммарный путь для каждого из шести вариантов.
Результаты рассмотрения возводим в таблицу 2.
Таблица 2 - Перспективы вариантов движения
| Варианты движения | Расстояние, км. | Перспективно или нет |
| А0 А2 А3 А1 | 150+150+350=650 | Нет |
| А0 А3 А2 А1 | 300+150+120=570 | Да |
| А0 А2 А4 А1 | Нет | |
| А0 А4 А2 А1 | Да | |
| А0 А3 А4 А1 | Нет | |
| А0 А4 А3 А1 | Да | |
| А0 А1 А3 А2 | Нет | |
| А0 А3 А1 А2 | Да | |
| А0 А1 А4 А2 | Нет | |
| А0 А4 А1 А2 | Да | |
| А0 А3 А4 А2 | Нет | |
| А0 А4 А3 А2 | Да | |
| А0 А1 А2 А3 | Да | |
| А0 А2 А1 А3 | Нет | |
| А0 А1 А4 А3 | Да | |
| А0 А4 А1 А3 | Нет | |
| А0 А2 А4 А3 | Нет | |
| А0 А4 А2 А3 | Да | |
| А0 А1 А2 А4 | Нет | |
| А0 А2 А1 А4 | Да | |
| А0 А1 А3 А4 | Да | |
| А0 А3 А1 А4 | Нет | |
| А0 А2 А3 А4 | Да | |
| А0 А3 А2 А4 | Нет |
После заполнения таблицы выделяем только перспективные варианты (их будет всего 12), дополняем их номером непосещенного населенного пункта и повторяем процедуру: определяем перспективность движения уже для четырех участков пути. Для этого к вычисленной длине перспективного пути (см. табл. 2) добавляем расстояние к непосещенному еще населенному пункту. Результаты вычислений заносим у табл. 3.
Таблица 3 - Перспективы выделенных вариантов движения
| Варианты движения | Расстояние, км. | Перспективно или нет |
| А0 А3 А2 А1 А4 | 570+200=770 | Нет |
| А0 А4 А2 А1 А3 | 470+350=820 | Нет |
| А0 А4 А3 А1 А2 | Нет | |
| А0 А3 А1 А2 А4 | Нет | |
| А0 А4 А1 А2 А3 | Да | |
| А0 А4 А3 А2 А1 | Да | |
| А0 А1 А2 А3 А4 | Да | |
| А0 А1 А4 А3А2 | Да | |
| А0 А4 А2 А3А1 | Нет | |
| А0 А2 А1 А4 А3 | Нет | |
| А0 А1 А3 А4 А2 | Нет | |
| А0 А2 А3 А4 А1 | Нет |
Аналогично предыдущему из табл. 3 выбираем четыре перспективных варианта.
Поскольку нам необходимо вернуться в начальный пункт, то выделены перспективные последовательности движения дополняем этим начальным пунктом A0. Вычисляем для них суммарные расстояния и заносим результаты у табл. 4.
Таблица 4 – Суммарные расстояния перспективных вариантов движения
| Варианты движения | Расстояние, км. | Перспективно или нет |
| А0 А4 А1 А2 А3А0 | 570+300=870 | Нет |
| А0 А4 А3 А2 А1А0 | 620+200=820 | Нет |
| А0 А1 А2 А3 А4 А0 | 620+100=720 | Да |
| А0 А1 А4 А3 А2 А0 | 700+150=850 | Нет |
Из таблицы видно, что есть один оптимальный маршрут прохождения коммивояжера А0 А1 А2 А3 А4 А0, который имеет минимальную из всех возможных маршрутов длину, ровную 720 км.
3. Метод ветвей и границь.
Расстояния между узлами разведения кабеля телевидения заданы следующей таблицей
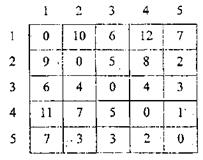
Решение: Превратим таблицу расстояний в матрицу Т, заменив нули на бесконечность, потому что возвращение в исходный пункт без охватывания всех других узлов разведения должно быть запрещено.
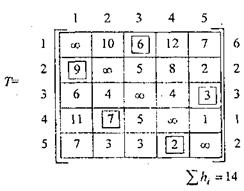
Задача сводится к поиску минимального гамильтонового цикла на полном графе, то есть к замкнутой задаче коммивояжера.
Определим минимальный путь методом простого пересмотра матрицы.
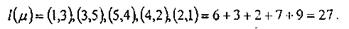
Полученное решение может оказаться не оптимальным, потому для решения задачи воспользуемся методом веток и границь.
Выполним сводку матрицы Т по строкам: 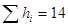 . Одержимо матрицу Т1. Возводим матрицу Т1 по столбцам:
. Одержимо матрицу Т1. Возводим матрицу Т1 по столбцам: 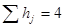
Уточнена оценка снизу
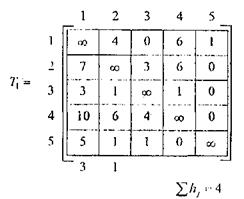
После сводки получаем матрицу Т2.
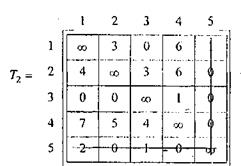
Для матрицы Т2 последовательное улучшение оценки снизу ∆(i, j):
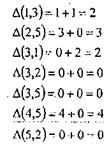
Наибольшее улучшение оценки снизу ∆(4,5)=4. Исключаем из Т2 четвертую строку и 5-й столбец и налагаем запрещение на дугу (5,4). Получаем матрицу Т3.
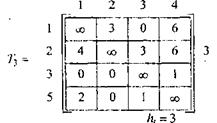 і
і 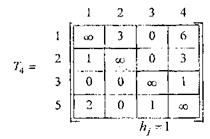
Выполняем сводку Т3 по строкам и столбцам. Получаем матрицу Т5. Теперь уточнена оценка снизу 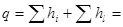 18 + 4 = 22.
18 + 4 = 22.
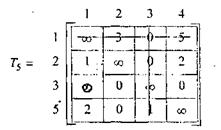
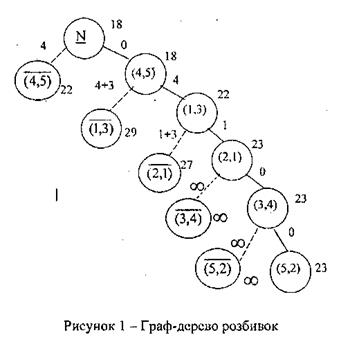
Последовательно строим дерево разбивок и заносим у него полученные величины.
Для Т5 улучшения оценки снизу:
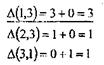
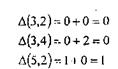
Наибольшее улучшение оценки снизу ∆(1,3)= 3. Исключаем из Т5 первую строку и 3-й столбец и налагаем запрещение на дугу (3,1). Получаем матрицу Т6. Выполняем сводку Т6 по строкам, получаем матрицу Т7. Уточнена оценка снизу 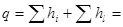 22+1=23.
22+1=23.
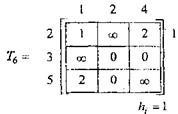
Для Т7 улучшения оценки снизу:
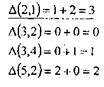
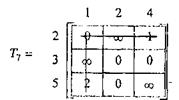
Наибольшее улучшение оценки снизу ∆(2,1)=3. Исключаем из Т7 вторую строку и 1-й столбец, а также налагаем запрещение на дугу (1,2). Получаем матрицу 2x2 – Т8.
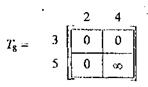
Для Т8 улучшения оценки снизу:
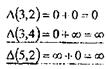
Дуть (3,4) и (5,2) включаем в гамильтонов путь и заносим в дерево разбивок.
Таким образом, кабель стоит прокладывать между пунктами в следующей последовательности:
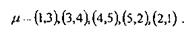
Минимальная затрата кабеля 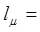 23 < 27, полученных методом простого пересмотра.
23 < 27, полученных методом простого пересмотра.
Контрольные вопросы.
1. Что такое граф? Пример
2. Какой граф называется ориентированным? Пример
3. Какой граф называется неориентируемым? Пример
4. Что называется петлей? Пример
5. Какие вершины называются смежными? Пример
6. Какое ребро называется инцидентным? Пример
7. Что такое степень вершины? Пример
8. Что такое кратность пары вершин? Пример
9. Что такое подграф? Пример
10. Что такое частный граф? Пример
11. Что называется путем в графе? Пример
12. Что называется длиной пути в графе? Пример
13. Что такое дерево? Пример
14. В чем заключается задание о коммивояжере? Пример
15. Способы решения задачи о коммивояжере
16. Каким способом в дискретной математике решают задачу коммивояжера?
Лекция № 12
Тема: «Реализация булевых функций с помощью логических схем»
План лекции
1. Основные логические операции и логические элементы
2. Распространённые логические операции и логические элементы
3. Функционально-полный набор логических элементов
4. Синтез и анализ логических функций и схем
1. Основные логические операции и логические элементы
Логический элемент в электронных схемах – это устройство, реализующее ту или иную логическую функцию. При этом логические сигналы 0 и 1 задаются разными уровнями напряжения. Сигнал логического нуля обычно представляется низким уровнем напряжения U0, логической единицы – высоким U1. Такая логика получила название положительной. В ряде случаев используют отрицательную логику, где логический нуль представляется высоким уровнем напряжения, а логическая единица – низким.
Логические схемы состоят из логических элементов, осуществляющих логические операции. Для изображения логических схем всегда используются условные графические обозначения элементов, описывающие только выполняемую элементами функцию и не зависящие от его схемы. В настоящее время в мире существует несколько общепринятых стандартов условных обозначений. Наиболее распространенными являются американский стандарт milspec 806В и стандарт МЭК 117-15 А, созданный Международной Электротехнической Комиссией. Часто в литературе используются также обозначения в европейской системе DIN 4070. В отечественной литературе условные обозначения элементов в основном соответствуют ГОСТ 2.743-82.
Конъюнкция(логическое умножение, операция И, AND): функция f принимает единичное значение только тогда, когда равны единице абсолютно все входные переменные. Следовательно, функция f принимает значение «0» только в том случае, если хотя бы один из входных переменных будет равен «0». В частности, для двух переменных х1 и х2 существует четыре различных сочетания, но только одному из них (х1=х2=l) соответствует единичное значение функции (табл.1).
Таблица 1
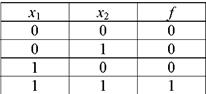
Условные графические обозначения элементов логического умножения по различным стандартам показаны на рис.1
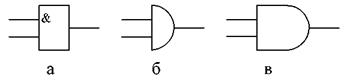
Рис. 1. Условные обозначения логического элемента И:
а) по ГОСТ и стандарту МЭК, б) по стандарту DIN, в) по стандарту milspec
Дизъюнкция(логическое сложение, операция ИЛИ, OR): функция f принимает единичное значение, если единице равна хотя бы одна из входных переменных (табл. 2). Следовательно, функция f принимает нулевое значение только в том случае, если все входные переменные будут равны «0».
Таблица 2
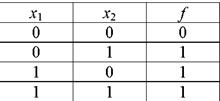
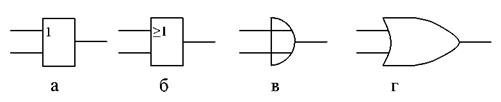
Рис. 2. Условные обозначения логического элемента ИЛИ:
а) по ГОСТ, б) по стандарту МЭК, в) по стандарту DIN, г) по стандарту milspec
Инверсия(отрицание, операция НЕ, NOT): функция одной переменной, принимает единичное значение, если входная переменная равна «0». Функция равна «0», если входная переменная равна «1» (табл. 3).
Таблица 3
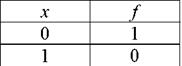

Рис. 3. Условные обозначения логического элемента НЕ:
а) по ГОСТ и стандарту МЭК, б) по стандарту DIN, в) по стандарту milspec
2. Распространённые логические операции и логические элементы
Наряду с простейшими распространены и более сложные логические элементы, сочетающие в себе несколько простейших операций. Такими являются логические элементы И-НЕ, ИЛИ-НЕ, ЭКВИВАЛЕНТНОСТЬ, ИСКЛЮЧАЮЩЕЕ ИЛИ и т.п.
Штрих Шеффера.Элемент И-НЕ реализует функцию «штрих Шеффера» двух переменных 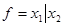 и имеет соответствующую таблицу истинности. Условное обозначение логического элемента И-НЕ в любом стандарте объединяет в себе обозначение элемента И и кружок, являющийся признаком элемента НЕ (рис. 4).
и имеет соответствующую таблицу истинности. Условное обозначение логического элемента И-НЕ в любом стандарте объединяет в себе обозначение элемента И и кружок, являющийся признаком элемента НЕ (рис. 4).
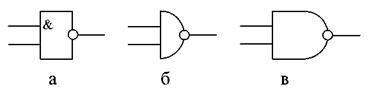
Рис. 4. Условные обозначения логического элемента И-НЕ:
а) по ГОСТ и стандарту МЭК, б) по стандарту DIN, в) по стандарту milspec
Стрелка Пирса.Элемент ИЛИ-НЕ реализует функцию «стрелка Пирса»: 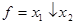 . Условные обозначения объединяют в себе обозначение элемента ИЛИ и кружок - символ операции отрицания НЕ (рис. 5).
. Условные обозначения объединяют в себе обозначение элемента ИЛИ и кружок - символ операции отрицания НЕ (рис. 5).
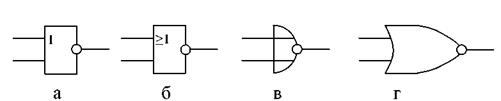
Рис. 5. Условные обозначения логического элемента ИЛИ-НЕ:
а) по ГОСТ, б) по стандарту МЭК, в) по стандарту DIN, г) по стандарту milspec
Эквивалентность.Элемент ЭКВИВАЛЕНТНОСТЬ (РАВНОЗНАЧНОСТЬ) описывается функцией 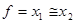 . В ней выходная переменная f принимает единичные значения только при равенстве входных переменных х1=х2. Функция имеет собственное обозначение и может быть выражена через простейшие логические операции:
. В ней выходная переменная f принимает единичные значения только при равенстве входных переменных х1=х2. Функция имеет собственное обозначение и может быть выражена через простейшие логические операции:
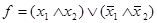
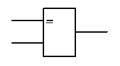
Рис. 6. Условное обозначение логического элемента ЭКВИВАЛЕНТНОСТЬ
3. Функционально-полный набор логических элементов
Набор логических элементов, достаточный для построения любой сколь угодно сложной логической схемы, называется функционально полным.
Функционально полным является набор элементов И, ИЛИ, НЕ. Из этого набора можно исключить некоторые элементы без нарушения функциональной полноты. В частности, функционально-полным считается набор из двух элементов И и НЕ. В этом случае для выполнения операции ИЛИ двух переменных x1 и x2 просто по уравнению 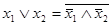 строится схема на трех элементах НЕ и одном элементе И.
строится схема на трех элементах НЕ и одном элементе И.
Аналогично, функционально полным является набор из элементов ИЛИ и элементов НЕ. На основании формулы де Моргана элемент И реализуется по уравнению
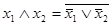 .
.
Свойство функциональной полноты используется при разработке и реализации многовходовых логических схем, так как реальные элементы интегральных схем выполняют или функцию И-НЕ (схемы транзисторно-транзисторной логики и КМОП технологии), или функцию ИЛИ-НЕ (схемы и-МОП и КМОП технологии). С помощью логических элементов ИЛИ-НЕ или И-НЕ можно собрать любую логическую схему. На таких элементах собран микропроцессор компьютера и другие логические устройства. Переход от логического умножения к логическому сложению (и обратно) и позволяет строить различные логические схемы, используя ограниченный функциональный набор логических элементов.
Для разработки структуры многовходовой логической схемы в заданном базисе применяют следующий алгоритм:
– составляется таблица истинности;
– по таблице истинности составляется булева функция в виде совершенной дизъюнктивной нормальной форме;
– используя правила булевой алгебры, карты Карно или другие способы минимизации, функция (если возможно) упрощается;
– полученное выражение приводят к заданному базису, применяя правило де Моргана. Если в качестве базы заданы элементы И-НЕ, правило де Моргана применяется к дизъюнкции, если ИЛИ-НЕ – к конъюнкции.
4. Синтез и анализ логических функций и схем
В цифровой электронике известны основные логические функции И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ, сложение по модулю 2 (исключающее ИЛИ), которые находят наиболее широкое применение при реализации цифровых устройств различного назначения. При представлении логической функции математическим выражением используют два вида ее представления: дизъюнктивная нормальная форма и конъюнктивная нормальная форма.
Элементарной конъюнкцией называется конъюнкция переменных или их отрицаний, в которой каждая переменная встречается не более одного раза. Дизъюнктивной нормальной формой (ДНФ) называется формула, имеющая вид дизъюнкции элементарных конъюнкций. Совершенная ДНФ – это ДНФ, каждая элементарная конъюнкция которой включает все переменные с отрицанием или без.
Для получения СДНФ по таблице истинности, в ней выделяют строки, в которых функция принимает единичные значения. Для каждой выделенной строки составляется конъюнкция всех входных переменных, причем сомножитель записывают со знаком инверсии, если переменная принимает в этой строке нулевое значение. Записывается логическая сумма всех составленных логических произведений, которые носят названия конституент единицы, или минтермов. Таким образом, СДНФ функции f содержит ровно столько конъюнкций, сколько единиц в таблице истинности, и все полученные конъюнкции соединяются знаками дизъюнкции. Для каждой функции СДНФ единственна (с точностью до перестановок переменных или конъюнкций).
Пример. Пусть задана логическая функция трёх переменных, которая равна единице в случае, если хотя бы две из входных переменных равны «1» (см. табл. 4). Требуется записать СДНФ этой функции.
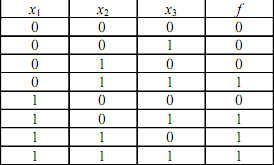
Для данной логической функции СДНФ имеет вид:
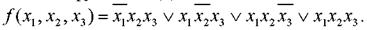
Конъюнктивной нормальной формой (КНФ) называется логическое произведение элементарных сумм, в каждую из которых аргумент или его отрицание входят один раз.
КНФ может быть получена из таблицы истинности: для каждого набора аргументов на котором функция равна «0» составляют элементарную сумму, причем переменные, значение которых равно «1», записываются с отрицанием. Полученные суммы, которые носят название конституент нуля, или макстермов, объединяют операцией логического умножения.
Пример. КНФ для функции из табл. 4 имеет вид:
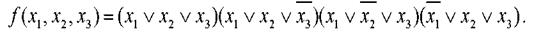
КНФ также называется совершенной, если каждая элементарная сумма содержит все переменные с инверсией или без.
Иногда удобнее пользоваться не самой логической функцией, а ее инверсией. В этом случае при использовании вышеописанных методик для записи СДНФ надо использовать нулевые, а для записи СКНФ – единичные значения функции.
Пример. Для логической функции из табл. 4 СДНФ и СКНФ инверсной функции имеют
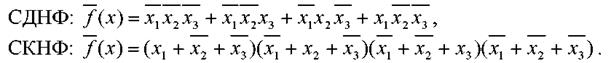
Дата добавления: 2021-09-25; просмотров: 732;











