Метод последовательных приближений

Неизохронность колебаний математического маятника связана с нелинейностью описывающего их уравнения (2.7). Общих методов решения нелинейных ДУ не существует, но есть несколько приближенных методов. Дальше мы рассмотрим один из таких методов - метод последовательных приближений.

Сначала проделаем на примере маятника, а потом приведём к общему виду. Разложим нелинейное слагаемое sin(x) в уравнении (2.7) в ряд Тейлора, ограничиваясь вторым слагаемым

,

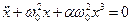(2.10)

здесь a = -1/6.

Зависимость периода колебаний от амплитуды (неизохронность колебаний) определяется коэффициентом a. Если a = 0 колебания чисто изохронные и период T = 2p/w₀.

Дальше воспользуемся теоремой из теории ДУ, что решение ДУ непрерывно зависит от параметра. Так как есть период, зависящий от w₀ то можно сказать, что w₀ - это параметр системы, который совпадает с частотой линейных колебаний. Введём параметр w - частота действующих (свободных) колебаний w = 2p/T(a). Мы знаем, что при a = 0, она совпадает с w₀, и непрерывно зависит от a, т. е. мы можем представить её в виде ряда по степеням a. Исторически сложилось (да и проще) раскладывать w²:

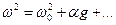
(2.11)

Считая нелинейность малой, мы ограничиваемся только первым слагаемым, содержащим a. Подставим (2.11) в (2.10), тогда, сохраняя только первые степени по a, получим

.

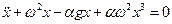(2.12)

Решение x(t) уравнения (2.12) тоже непрерывно зависит от параметра a, причём при a = 0

.

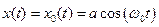В силу непрерывности решения по a, можно записать, ограничиваясь только первой степенью a, что при a ¹ 0,

.

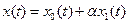Подставим это решение в (2.12), пренебрегая степенями a со второй включительно

,

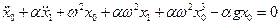и, учитывая уравнение нулевого приближения для x₀

,

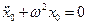получим окончательное уравнение первого приближения

.

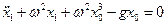В нашем случае, выбирая начальные условия в виде t = 0, x = a, 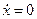, находим решение уравнения нулевого приближения

.

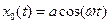Уравнение первого приближения соответственно будет

.

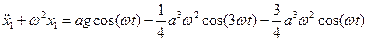(2.13)

У нас получилось линейное уравнение, в правой части которого стоят гармонические силы. Получилось, что на систему с собственной частотой w действуют два гармонических процесса с частотами w и 3w. Так как потерь нет, то колебания совершаются с бесконечной амплитудой (на частоте w резонанс), поэтому, чтобы такого не было, необходимо положить

,

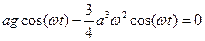тогда уравнение первого приближения примет вид:

.

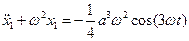(2.14)

Из предыдущего соотношения находим, что 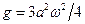. Тогда, подставив его в (2.11), получим

,

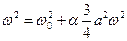следовательно

.

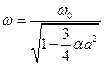(2.15)

Решение уравнения первого приближения будет иметь вид:

,

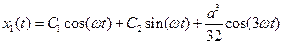где С₁ и С₂ - произвольные постоянные. Тогда полное решение (2.10) в первом приближении запишется следующим образом:

.

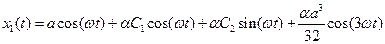Значения произвольных постоянных можно найти, требуя от этого решения, чтобы оно удовлетворяло тем же начальным условиям, т. е. 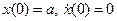, тогда окончательно с учётом формулы (2.15)

.

(2.16)

Из найденного соотношения видно, что колебания не изохронные и в них присутствуют высшие гармоники. Для математического маятника частота свободных колебаний убывает с ростом их амплитуды.