Статическая САР угловой скорости

Эта система подробно изложена в описаниях по лабораторным работам.

Она служит для стабилизации угловой скорости ведущего вала аудиомагнитофона. На самом деле, для аудиомагнитофона важна поступательная (линейная) скорость транспортирования ленты. Если нет проскальзывания магнитной ленты, то при угловой скорости Ω = const будет постоянна и линейная скорость V_л.

Если нет проскальзывания, то можно написать такое соотношение:

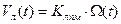
Эта система очень хорошо стабилизирует угловую скорость, но если будет проскальзывание, то с линейной будет не ахти.

В этой системе используется принцип регулирования по ошибке.

Изобразим структурную схему САР.

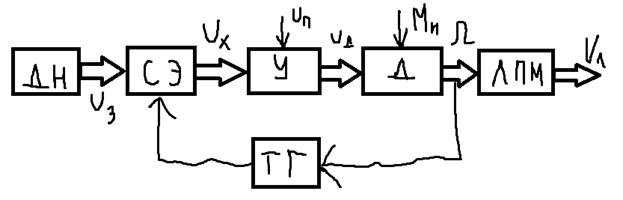
ДН – делитель напряжения

СЭ – сравнивающий элемент (нелинейный!)

У – усилитель

Д – двигатель

М_Н – момент нагрузки

ЛПМ – лентопротяжный механизм.

Д+ЛМП=ОР

ТГ – тахогенератор

Усиление в данном случае – сигнал ошибки показывает, какую долю от питания использовать.

Небольшие изменения напряжение питания не приводят к большим изменениям. Возмущением в данном случае является момент нагрузки. Задающее воздействие – задающее напряжение (u_з является g). Делитель напряжения – задающий элемент. Сравнивающий элемент выполнен на операционных усилителях. Тахогенератор – датчик угловой скорости (регулируемая величина – угловая скорость). Используется коллекторный двигатель постоянного тока. Усилитель реализован на двух транзисторах.

Чтобы понять принцип действия, надо располагать математической моделью всех систем.

1) модель коллекторного двигателя постоянного тока с учётом действия моментов нагрузки при условии пренебрежении индуктивностью обмотки якоря L_я (с учётом обмотки получается дифференциальное уравнение второго порядка).

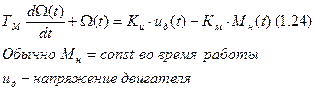
Т_М – электромеханическая постоянная времени.

Коэффициенты – коэффициенты передачи двигателя по напряжению и по моменту нагрузки на нулевой частоте.

2) модель лентопротяжного механизма.

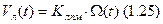
3) модель операционного усилителя.

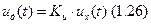
4) модель сравнивающего устройства.

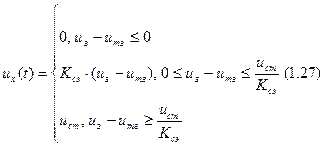
u_ст – напряжение пробоя стабилитрона (он в цепи обратной цепи ОУ).

Эта формула справедлива с определённых моментов.

5) модель тахогенератора.

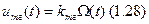
23.10.2012

Теперь уточнение к модели двигателя.

Три закона в основе двигателей:

I. Уравнение динамики для вращательного движения (второй закон Ньютона):

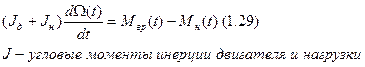
Чтобы создать движение объекта с ускорением, надо, чтобы равнодействующая всех сил была не равна нулю. А для вращательного движения надо, чтобы сумма всех моментов была отлична от нуля.

Для поступательного движения будет не момент инерции, а масса.

Для рассматриваемого нами двигателя надо, чтобы эти моменты сравнялись, ведь в итоге должна получиться постоянная скорость движения ленты.

NB! Линейный двигатель предназначен для создания поступательного движения.

II. Вращающий момент появляется за счёт закона Ампера:

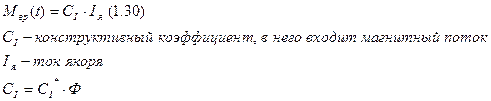
III. Пусть между зажимами обмотки двигателя действует напряжение u_д. Обмотка якоря характеризуется активным и реактивным сопротивлением.

Важно! Ток якоря почти равен нулю.

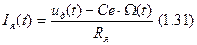
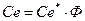
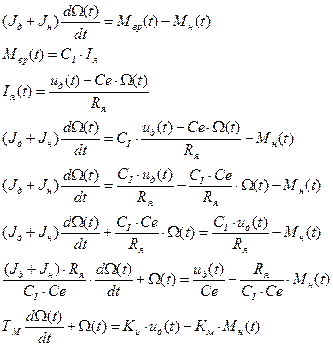
Использование нелинейного сравнивающего элемента (формула 1.27) позволяет осуществить пуск двигателя с максимальным подведённым напряжением.

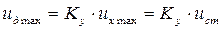
Это обеспечивает малое время переходного процесса.

Сейчас сие докажем.

В первый момент, когда подводится питание к системе, угловая скорость равна нулю. Значит, напряжение на выходе тахогенератора равно нулю, а сигнал ошибки

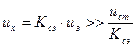
Значит, и получается максимальное напряжение.

При этом используемая ООС в начале как бы разомкнута, и принцип по отклонению не работает.

Двигатель начинает разгоняться, угловая скорость начинает возрастать, напряжение на выходе тахогенератора увеличивается, и наступает момент времени t₁, когда разница между напряжениями станет равно точно u_ст/K_сэ, и с этого момента происходит переход на другую модель, обратная связь замыкается и начинает полноценно работать принцип регулирования по отклонению.

В этой системе рассматривается только одно возмущение – момент нагрузки на валу двигателя.

Перед проектированием указывают диапазон возможных значений моментов нагрузки, которые могут возникать, а именно указывают M_{н min} и M_{н max}. Также задаётся диапазон возможных требуемых значений угловой скорости Ω_min и Ω_max.

При проектировании исходят из того, что угловой момент в течение времени является постоянным. И требуется, чтобы после переходных процессов угловая скорость была постоянной.

А какое надо выбирать задающее напряжение? Его будем выбирать из условия:

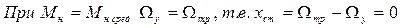
Так как система стабилизации, то u_з должно быть постоянным. Таким образом, по окончании переходного процесса надо получить уравнения статики.

Составим структурную модель для статического режима системы.

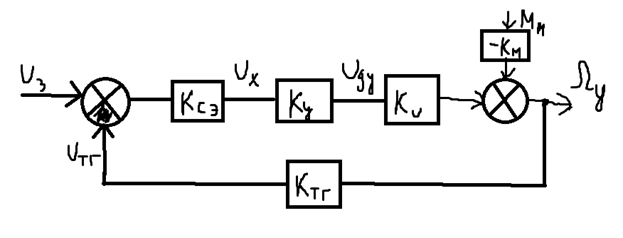
Используя материал, касающийся принципу регулирования по отклонению, вывести формулу для установившегося значения угловой скорости.

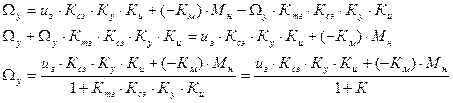
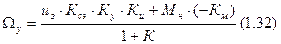
Из 1.32 вывести формулу для u_з. Она будет 1.33.

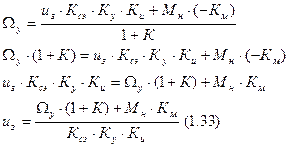
Также вывести x_ст = -К_м*(М_{н сред} – М_н)/(1+К) (1.34).

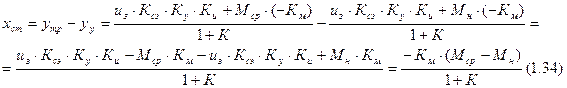
В этой системе только при одном значении момента нагрузки статическая ошибка будет равна нулю. Система также нелинейная.

30.10.2012

Качественно рассмотрим график изменения скорости.

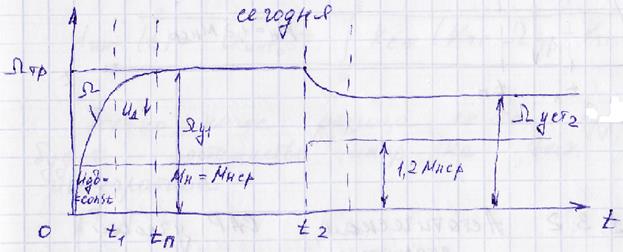
1. Задаёмся М_н.

Почему, начиная с момента времени t_п, будет установившееся значение? Потому что М_н = М_вр => ускорение будет нулевым, после этого угловая скорость становится постоянной.

Допустим, что в момент времени t₂ момент нагрузки возрос на 20%.

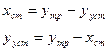
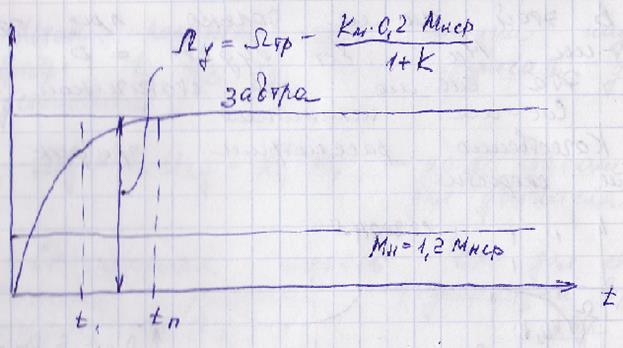
В астатической системе будет возврат Ω_у к требуемому значению.

Возрос момент нагрузки, ускорение падает, подводимое напряжение возрастает, ток якоря возрастает, и следовательно момент вращения возрастает, и когда М_вр = 1,2М_н, заканчивается переходной процесс.