Типовые примеры и методы их решения
Пример 2.5.1. На вклад начисляются сложные проценты: а) ежегодно; б) ежеквартально; в) ежемесячно. Какова должна быть годовая номинальная процентная ставка, при которой происходит реальное наращение капитала, если ежемесячный темп инфляции составляет 3%?
Решение. а) Обозначим через 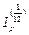 среднемесячный (т.е. за 1/12 года) индекс инфляции, тогда
среднемесячный (т.е. за 1/12 года) индекс инфляции, тогда 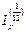 =1,03 и по формуле (42) при k = 12 находим индекс инфляции за год:
=1,03 и по формуле (42) при k = 12 находим индекс инфляции за год:
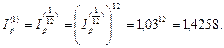
Пусть r - процентная ставка при ежегодном начислении ножных процентов, тогда в соответствии с формулой (104) значение ставки, лишь нейтрализующей действие инфляции, находится из равенства 1 + r = 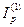 (т.е. множитель наращения за год приравнивается к годовому индексу инфляции). Таким образом:
(т.е. множитель наращения за год приравнивается к годовому индексу инфляции). Таким образом:
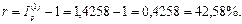
Следовательно, реальное наращение капитала будет происходить только при процентной ставке, превышающей 42,58% годовых.
б) При ежеквартальном начислении сложных процентов для определения номинальной ставки, лишь нейтрализующей действие инфляции, согласно формуле (104) пользуемся равенством 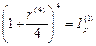 откуда:
откуда:
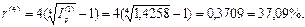
Таким образом, положительная процентная ставка при ежеквартальном начислении сложных процентов превышает 37,09% годовых.
в) В случае ежемесячного начисления процентов пользуемся равенством 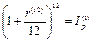 откуда:
откуда:
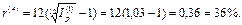
Итак, в данной ситуации реальное наращение капитала происходит при номинальной процентной ставке, большей чем 36% годовых. В этом случае ответ можно было дать сразу, поскольку для осуществления реального наращения капитала его относительный рост за месяц должен превышать темп инфляции за это же время. Следовательно, 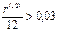 , поэтому r(12) > 0,36.
, поэтому r(12) > 0,36.
Заметим, что величину сложной процентной ставки, лишь нейтрализующей действие инфляции, можно найти из формулы (105), при r(m) = 0:
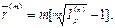
Полагая n = 1, ответы для случаев а), б), в) получим соответственно при m = 1, 4, 12.
Пример 2.5.2. Номинальная процентная ставка, лишь компенсирующая при наращении действие инфляции, составляет 52% годовых. Определите полугодовую инфляцию, если начисление сложных процентов осуществляется каждый квартал.
Решение. Приравняем годовой индекс инфляции 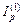 к множителю наращения за год. Полагая r(4) = 0,52, получим:
к множителю наращения за год. Полагая r(4) = 0,52, получим:
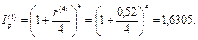
Поэтому индекс инфляции за полгода (0,5 года) составит:
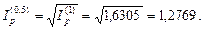
Следовательно, темп инфляции за полгода в среднем равен 27,69%.
Пример 2.5.3. На некоторую сумму в течение трех лет будут начисляться непрерывные проценты. По прогнозам инфляция в это время за каждый год последовательно составит 15, 20 и 10%. Какова должна быть сила роста за год, чтобы сумма по своей покупательной способности не уменьшилась?
Решение. Поскольку индекс инфляции за первый год равен 1,15, за второй – 1,2 и за третий – 1,1, то индекс инфляции за 3 года составит:
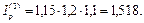
Пусть 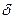 – сила роста за год, позволяющая первоначальной сумме только сохранить свою покупательную способность. Приравнивая индекс инфляции за три года к множителю наращения за это же время, получим
– сила роста за год, позволяющая первоначальной сумме только сохранить свою покупательную способность. Приравнивая индекс инфляции за три года к множителю наращения за это же время, получим 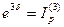 , отсюда
, отсюда
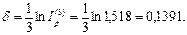
Следовательно, сила роста (интенсивность наращения) превышать 13,91% за год.
Пример 2.5.4. На вклад в течение 15 месяцев начисляются проценты: а) по схеме сложных процентов; б) по смешанной схеме. Какова должна быть процентная ставка, при которой происходит реальное наращение капитала, если каждый квартал цены увеличиваются на 8%?
Решение. а) Так как темп инфляции за каждый квартал равен 8%, то индекс инфляции за каждый квартал (0,25 года) равен 1,08. Поэтому индекс инфляции за 15 месяцев (1,25 года, или 5 кварталов) составит:
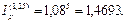
Обозначим через r искомую годовую процентную ставку и приравняем этот индекс инфляции к множителю наращения при использовании схемы сложных процентов:
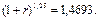
Отсюда:
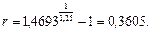
Таким образом, в этом случае ставка должна превышать 36,05% годовых.
При рассмотрении этого случая можно было рассуждать и таким образом. При инфляции 8% за каждый квартал годовой темп инфляции составит 1,084–1= =0,3605=36,05%, Реальное же наращение капитала будет происходить, если годовая процентная ставка превышает годовой темп инфляции, т.е. r > 36,05% .
б) Пусть теперь применяется смешанная схема. Приравнивая индекс инфляции за 1 ,25 года к множителю наращения, получим квадратное уравнение относительно r :
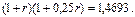
Решая уравнение, определяем корни: r1 = -5,3508, r2 =0,3508. Очевидно, что по смыслу первый корень не подходит. Следовательно, при использовании смешанной схемы ставка должна превышать 35,08% годовых. "Граничное" значение ставки в этом случае получили почти на 1 % меньше, чем в предыдущем, что объясняется большей эффективностью смешанной схемы начисления по сравнению со схемой сложных процентов.
Обратим внимание, что для ответа на вопрос в данном случае необходимо фактически решить неравенство:
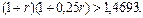
Если применяется иного вида смешанная схема наращения, то для определения процентной ставки r получим другое уравнение. В частности, при использовании схемы сложных процентов для двух лет и затем при учете полученной суммы "на 100" за 0,75 года приходим к уравнению:
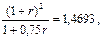
преобразуя которое получаем квадратное уравнение с корнями r1 = -1,2681 , r2 = =0,3701 . Отбрасывая первый корень, делаем вывод, что при данной схеме начисления процентов ставка должна превышать 37,01% годовых. Такой же результат получим, решая неравенство 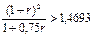 и отбрасывая в полученном ответе отрицательную область.
и отбрасывая в полученном ответе отрицательную область.
Пример 2.5.5. На вклад 28 тыс. руб. ежеквартально начисляются сложные проценты по номинальной годовой процентной ставке 40%. Оцените сумму вклада через 21 месяц с точки зрения покупательной способности, если ожидаемый темп инфляции – 2% в месяц. Какова должна быть величина номинальной положительной процентной ставки? Как изменится ситуация, если темп инфляции будет 3,5% в месяц?
Решение. По формуле (58) за n =1,75 года (21 месяц) сумма вклада составит:
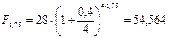 тыс. руб.
тыс. руб.
Индекс инфляции за 1,75 года при темпе инфляции 2% в месяц находим по формуле (42):
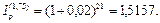
Применяя формулу (104), находим величину вклада с точки фения ее покупательной способности:
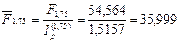 тыс. руб.
тыс. руб.
Вычитая из этой величины первоначальную сумму вклада, найдем реальный доход владельца вклада:
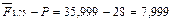 тыс. руб.
тыс. руб.
Положительная процентная ставка r(4) должна удовлетворять неравенству:
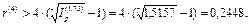
Таким образом, при темпе инфляции 2% в месяц и ежеквартальном начислении сложных процентов реальное наращение капитала будет происходить только при процентной ставке, превышающей 24,48%. А поскольку номинальная процентная ставка удовлетворяет этому условию, то владелец вклада, несмотря на инфляцию, получает реальный доход.
Естественно, к такому же ответу можно было прийти, используя условие: относительный рост вклада за квартал должен превышать темп инфляции за это время, т.е. должно выполняться неравенство:
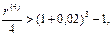
решая которое находим r(4) > 0,2448.
При темпе инфляции 3,5% в месяц: 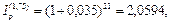
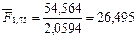 тыс. руб. реальный доход вкладчика составит 26,495–28=- 1,505 тыс. руб., т.е. в этом случае вкладчик с точки зрения покупательной способности потерпит убытки. В данных условиях для положи тельной процентной ставки должно выполняться неравенство
тыс. руб. реальный доход вкладчика составит 26,495–28=- 1,505 тыс. руб., т.е. в этом случае вкладчик с точки зрения покупательной способности потерпит убытки. В данных условиях для положи тельной процентной ставки должно выполняться неравенство 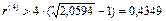 , т.е. r(4) > 43,49% . Следовательно, номинальная процентная ставка (40%) меньше положительной процентной ставки.
, т.е. r(4) > 43,49% . Следовательно, номинальная процентная ставка (40%) меньше положительной процентной ставки.
Пример 2.5.6. Кредит 120 тыс. руб. выдается сроком на 4 года при условии начисления сложных процентов. Какова должна быть процентная ставка по кредиту, чтобы реальная доходность кредитной операции составляла 18% годовых по ставке сложных процентов? Чему будет равна погашаемая сумма? Расчетный индекс цен за срок кредита принимается равным 2,3.
Решение. Полагая в формуле (105) m = 1, r(m) =0,18, n = 4, 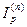 = 2,3 , находим:
= 2,3 , находим:
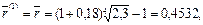
т.е. ставка 45,32% годовых при ежегодном начислении сложных процентов и индексе цен, равном 2,3, обеспечивает реальную доходность в 18% годовых.
Погашаемую сумму находим по формуле (55) при Р = 120 тыс. руб., n = 4, r = =0,4532:
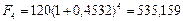 тыс. руб.
тыс. руб.
Пример 2.5.7. На выданный кредит в 90 тыс. руб. в течение трех лет будут начисляться сложные проценты: а) каждые полгода; б) ежеквартально; в) ежемесячно. Какую номинальную годовую процентную ставку необходимо установить, чтобы происходило реальное наращение капитала по номинальной процентной ставке 24% годовых, если ожидается темп инфляции 14% в год? Определите наращенную сумму, которую необходимо будет вернуть.
Решение. Во всех случаях при определении величины устанавливаемой процентной ставки можно воспользоваться формулой (105). Однако эта формула в силу соотношения 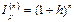 , справедливого для данного примера, приобретает более простой вид:
, справедливого для данного примера, приобретает более простой вид:

а) Полагая m = 2, r(2) = 0,24, h = 0,14, из последней формулы получим:
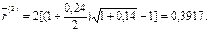
Следовательно, возвращаемая через 3 года сумма составит:
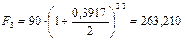 тыс. руб.
тыс. руб.
б) В этом случае m = 4 , r(4) = 0,24, и поэтому величины устанавливаемой номинальной процентной ставки и возвращаемой суммы равны:
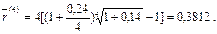
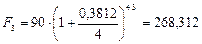 тыс. руб.
тыс. руб.
в) Полагая m = 12, r(12) = 0,24 , получим:
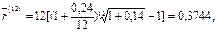
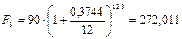 тыс. руб.
тыс. руб.
Пример 2.5.8. На какой срок при годовом темпе инфляции 20% необходимо поместить имеющуюся денежную сумму под; а) сложную процентную ставку 36% годовых; б) сложную учетную ставку 36% годовых; в) силу роста 36% за год, чтобы от реально (по своей покупательной способности) увеличилась в 1,6 раза?
Решение. а) Обозначим через Р величину денежной суммы, через r – годовую процентную ставку, через h – темп инфляции за год и воспользуемся формулой (104), принимающей и этом случае следующий вид:
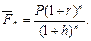
Полагая r = 0,36, h = 0,2 получим равенство:
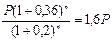
из которого следует уравнение для определения искомого срока:
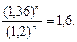
Логарифмируя это уравнение, получим:
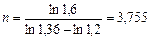 года.
года.
б) Для сложной годовой учетной ставки d формула (104) принимает вид:
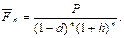
При d = 0,36 приходим к уравнению:
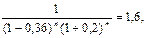
откуда:
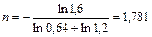 года.
года.
в) Обозначим через 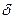 силу роста, тогда:
силу роста, тогда:
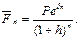
Следовательно, при 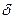 = 0,36 получаем уравнение:
= 0,36 получаем уравнение:
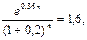
из которого следует:
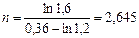 года.
года.
При решении этого примера можно было вначале вывести общую формулу для определения срока. Полагая в формуле (110) 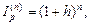 ,
, 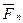 =1,6P и разрешая полученное уравнение относительно n, находим:
=1,6P и разрешая полученное уравнение относительно n, находим:
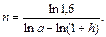
Затем вместо а последовательно подставляем 1 + r, 1 – d и 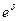 .
.
Пример 2.5.9. Определите реальную силу роста за год в условиях начисления непрерывных процентов и при годовом темпе инфляции 40%, если исходная сила роста составляет 50% за год. Какова должна быть сила роста, чтобы при такой инфляции обеспечить реальную доходность согласно исходной непрерывной ставке 50%?
Решение. Полагая в формуле (110) n = 1, 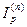 =1,4,
=1,4, 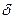 = 0,5, получим:
= 0,5, получим:
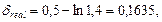
т.е. реальная интенсивность наращения при начислении непрерывных процентов составляет 16,35% за год.
Чтобы иметь доходность согласно силе роста 50% в условиях инфляции, необходимо установить непрерывную ставку большую, чем 50%. Значение такой ставки находим по формуле (109):
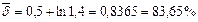
Заметим, что даже при темпе инфляции 50% сила роста 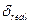 будет все еще положительной непрерывной ставкой. Действительно:
будет все еще положительной непрерывной ставкой. Действительно:
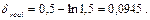
Пример 2.5.10. При выдаче кредита на несколько лет на условиях начисления сложных процентов банк желает обеспечить реальную доходность такой финансовой операции в 16% годовых по сложной ставке процентов. Какую процентную ставку по кредиту должен установить банк, если инфляция прогнозируется в среднем 10% в год?
Решение. Для определения искомой процентной ставки воспользуемся формулой Фишера (111) при r = 0,16 и h = 0,1:
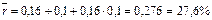
При малом темпе инфляции и невысокой процентной ставке применяют и приближенную формулу: 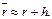 . В данном случае
. В данном случае 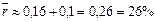 и разница в 1,6% при достаточно больших суммах ощутима. Конечно, для должника желательно использование приближенной формулы, а для банка, предоставляющего кредит, выгоднее применять точную формулу (111).
и разница в 1,6% при достаточно больших суммах ощутима. Конечно, для должника желательно использование приближенной формулы, а для банка, предоставляющего кредит, выгоднее применять точную формулу (111).
Полезно отметить, что при решении примера можно было воспользоваться формулой (105). Действительно, так как m = 1, 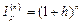 , то
, то
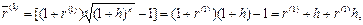
т.е. формула Фишера является частным случаем формулы (105). При n = 1 формула (44) совпадает с формулой Фишера.
Пример 2.5.11. Определите реальную доходность в виде процентной ставки при помещении денежных средств на год под сложную процентную ставку 45% годовых, если предполагаемый уровень инфляции за год составит: а) 15%; б) 45%; в) 60%.
Решение. Воспользуемся формулой (106), которая в условиях примера примет вид ( m = 1 , n = 1 , 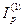 = 1 + h ):
= 1 + h ):
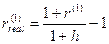 или
или 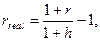
где 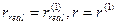 . Во всех случаях r = 0,45.
. Во всех случаях r = 0,45.
а) При инфляции h =0,15 получим:
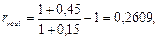
т.е. реальный доход от финансовой операции составит 26,09% от каждой единицы вложенных средств.
б) При h = 0,45, как и следовало ожидать, rreal = 0, т.е. ставка 45% лишь нейтрализует действие инфляции.
в) Полагая h = 0,6, получим:
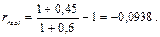
Таким образом, при инфляции 60% данная финансовая операция будет приносить убыток, т.е. реально по своей покупательной способности помещенные денежные средства уменьшатся на 9,38%.
Обратим внимание, что при решении этого примера можно было воспользоваться и формулой (46). Очевидно, и формула Фишера позволяет ответить на вопросы примера. В частности, подставляя в нее значения процентной ставки и инфляции первого случая (в обозначениях формулы Фишера: 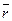 = 0,45, h = 0,15), получим уравнение 0,45 = r + 0,15 + 0,15r, откуда
= 0,45, h = 0,15), получим уравнение 0,45 = r + 0,15 + 0,15r, откуда 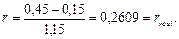
Пример 2.5.12. Банк предлагает клиентам поместить деньги на депозит на 3 года под процентную ставку 40% годовых с ежемесячным начислением сложных процентов. Найдите реальную доходность такого предложения в виде годовой эффективной процентной ставки, если предполагаемый индекс цен за 3 года составит 2,1. Чему будет равна реальная доходность при полугодовом начислении сложных процентов?
Решение. Полагая n = 3, 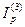 =2,1, m = 12, r(12)=0,4, по формуле (106) определяем реальную номинальную процентную ставку:
=2,1, m = 12, r(12)=0,4, по формуле (106) определяем реальную номинальную процентную ставку:
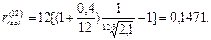
Поэтому согласно формуле (63) реальная доходность в виде годовой эффективной процентной ставки составит:
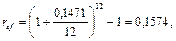
т.е. 15,74% годовых. Если же инфляцию не учитывать, то
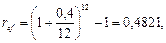
что существенно больше, чем реальная доходность.
Можно было решить пример и несколько иным способом. Вначале, обозначая величину вклада через Р, по формуле (104) при 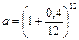 определяем наращенную сумму с точки зрения ее покупательной способности:
определяем наращенную сумму с точки зрения ее покупательной способности:
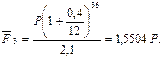
Затем по формуле (64) находим доходность:
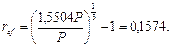
Естественно, получили такой же ответ. Если при втором способе решения действия провести в общем виде, то полученная формула покажет, что на самом деле можно было сделать меньше вычислений. Действительно, поскольку 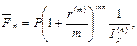 то
то 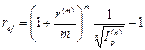 и поэтому:
и поэтому:
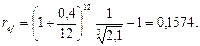
Воспользуемся последней формулой для нахождения реальной доходности предложения банка при полугодовом начислении сложных процентов:
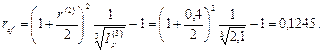
Естественно, с уменьшением количества начислений сложных процентов уменьшается и доходность.
Пример 2.5.13. Вексель на сумму 45 тыс. руб. был учтен за 3 года до срока погашения, и предъявитель векселя получил 18 тыс. руб. Найдите реальную доходность этой финансовой операции в виде эффективной учетной ставки, если среднегодовой темп инфляции ожидается равным 14%.
Решение. Так как индекс цен за 3 года равен 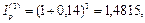 , то по своей покупательной способности 45 тыс. руб. через 3 года составят величину
, то по своей покупательной способности 45 тыс. руб. через 3 года составят величину 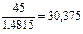 тыс. руб. Подставляя в формулу (75) n = 3, Р = 18, F3 = 30,375, находим:
тыс. руб. Подставляя в формулу (75) n = 3, Р = 18, F3 = 30,375, находим:
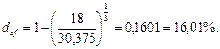
Можно было решить этот пример, определяя вначале реальную доходность в виде годовой эффективной процентной ставки:
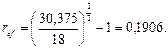
А затем по формуле (26) при n = 1, r = ref или по формуле (3) при rt = ref найти эквивалентную ставку def:
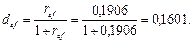
Пример 2.5.14. Господин N получил в банке кредит на 4 года, при этом банком были удержаны комиссионные в размере 1,5% от величины кредита. Определите действительную доходность для банка такой финансовой операции в виде годовой эффективной процентной ставки, если банк начисляет каждые полгода сложные проценты на исходную сумму кредита по номинальной процентной ставке 42% годовых и прогнозируемый ежегодный темп инфляции составляет 28%.
Решение. Обозначим через Р величину кредита, тогда величина удержанных комиссионных составит 0,015Р, и, следовательно, господину N будет выдана сумма Р – 0,015Р = 0,985P. За 4 года с учетом инфляции величина кредита вместе с начисленными процентами составит (формулы (42) и (104)):
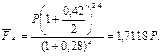
Теперь доходность финансовой операции в виде эффективной процентной ставки находим по формуле (64):
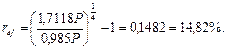
В данном случае вычисления можно несколько сократить, если 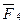 не вычисляя сразу подставить в формулу для определения ref:
не вычисляя сразу подставить в формулу для определения ref:
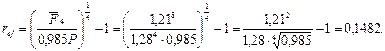
Если инфляции нет, то
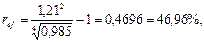
т.е. доходность, конечно, больше, чем при наличии инфляции.
Пример 2.5.15. Под какую годовую номинальную процентную ставку на условиях начисления ежемесячно сложных процентов необходимо поместить денежную сумму, чтобы она реально (по своей покупательной способности) увеличилась за год на 25% с учетом уплаты налога на проценты, если ставка налога на проценты равна 12% и ежеквартальный темп инфляции равен 10%? Если наращение осуществляется по годовой номинальной учетной ставке с ежеквартальным начислением сложных процентов, то какой величины должна быть эта ставка?
Решение. Годовой индекс инфляции определяем по формуле (42):
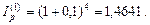
Обозначим через Р величину денежной суммы, через r(12) – искомую процентную ставку. Наращенная сумма без учета инфляции в соответствии с формулой (58) составит 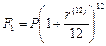 и, следовательно, начисленные проценты равны:
и, следовательно, начисленные проценты равны:
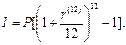
С этой величины в счет уплаты налога на проценты пойдет сумма 0,12I, и поэтому после уплаты величина наращенной суммы составит:
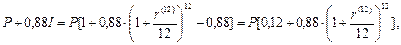
а с учетом инфляции:
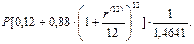
Полученная сумма должна быть больше исходной на 25%, т.е. в 1,25 раза. Таким образом:
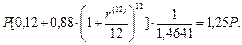
Сокращаем обе части уравнения на Р и решаем уравнение относительно r(12). После ряда алгебраических преобразований получим:
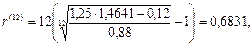
т.е. r(12)=68,31% годовых.
Если наращение осуществляется по учетной ставке d(4) используя формулу (77), получим:
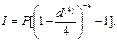
После уплаты налога величина наращенной суммы составит:
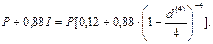
Поскольку полученная сумма по своей покупательной способности должна быть больше исходной в 1,25 раза, то
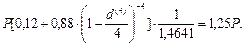
Сокращая обе части уравнения на Р и решая уравнение относительно d(4), получим:
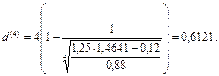
Заметим, что такой же результат получим, и определяя по формуле (92) учетную ставку d(4), эквивалентную процентной ставке r(12) =68,31% при m = 4, l = 12:
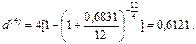
Дата добавления: 2020-10-25; просмотров: 711;











