Типовые примеры и методы их решения
Пример 3.2.1. В течение 4 лет на счет в банке ежедневно будут поступать одинаковые платежи, каждый год составляя и сумме 10 тыс. руб. Определите сумму, накопленную к концу четвертого года при использовании процентной ставки 15% годовых, если начисление сложных процентов осуществляется: а) ежегодно; б) ежемесячно.
Решение. а) Полагаем n = 4, m = 1, r = 15%. Поскольку платежи поступают достаточно часто, будем считать, что они поступают непрерывным образом. Тогда можно воспользоваться формулой (134) при  = 10 тыс. руб.:
= 10 тыс. руб.:
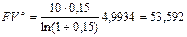 тыс. руб.
тыс. руб.
Сравним этот результат со значением, полученным по формуле (122), полагая, что в году 360 дней и дан аннуитет постнумерандо. Так как р = 360, 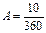 , получим:
, получим:
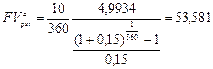 тыс. руб.
тыс. руб.
Видим, что полученные величины отличаются незначительно (всего на 11 руб.). Кстати, считая, что имеем дело с аннуитетом пренумерандо, по формуле (126) находим:
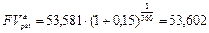 тыс. руб.
тыс. руб.
Эта величина также мало отличается от 53,592 тыс. руб. (на 10 руб.). Значения же 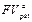 и
и  незначительно отличаются друг от друга, поскольку при частом (в данном случае - ежедневном) поступлении денег разница между аннуитетами постнумерандо и пренумерандо начинает исчезать.
незначительно отличаются друг от друга, поскольку при частом (в данном случае - ежедневном) поступлении денег разница между аннуитетами постнумерандо и пренумерандо начинает исчезать.
б) Так же как и в предыдущем случае, будем считать, что платежи поступают непрерывным образом. Поскольку при m = 12 ( и поэтому 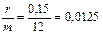 ) табличным значением коэффициента наращения аннуитета воспользоваться нельзя, перед вычислением преобразуем немного формулу (134):
) табличным значением коэффициента наращения аннуитета воспользоваться нельзя, перед вычислением преобразуем немного формулу (134):
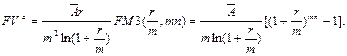
Отсюда:
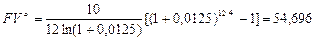 тыс. руб.
тыс. руб.
Предполагая же, что в условии говорится о постоянном аннуитете постнумерандо или пренумерандо, соответственно по формулам (122) и (126) получим:
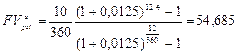 тыс. руб.;
тыс. руб.;
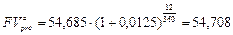 тыс. руб.
тыс. руб.
Видим, что вычисленные значения мало отличаются от 54,696 тыс. руб.
Пример 3.2.2. Фирма намеревается выпускать некоторую продукцию в течение трех лет, получая ежегодно выручку в размере 30 млн. руб. Предполагается, что продукция в течение года будет продаваться более или менее равномерно. Оцените ожидаемые денежные поступления, если применяется непрерывная ставка 20% за год.
Решение. Поскольку в условии говорится о более или меле равномерном распределении продаж в течение года, то логично предполагать, что интенсивность потока выручки будет в каком то мере постоянной величиной, равной 30 млн. руб. в год. Считая, что денежные поступления происходят непрерывно, воспользуемся формулами (137) и (138), определяющими соответственно будущую и приведенную стоимости непрерывного аннуитета. Полагая 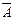 = 30 млн. руб., п = 3,
= 30 млн. руб., п = 3, 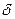 = 0,2, получим:
= 0,2, получим:
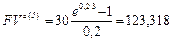 млн. руб.;
млн. руб.;
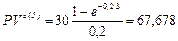 млн. руб.
млн. руб.
Конечно, при определении 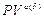 можно было воспользоваться уже найденным значением
можно было воспользоваться уже найденным значением 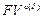 и формулой (78), из которой следует:
и формулой (78), из которой следует:
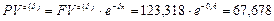 млн. руб.
млн. руб.
Пример 3.2.3. Финансовая компания в течение пяти лет к соответствии со своими обязательствами должна выплачивать вкладчикам по 20 млн. руб. ежегодно. Какой суммой должна располагать компания, чтобы иметь возможность выполнить обязательства, если норма доходности составляет 30% за год и выплаты происходят постоянно и достаточно равномерно?
Решение. Полагая, что выплаты происходят непрерывно с постоянной интенсивностью (т.е. моделируя ситуацию с помощью непрерывного аннуитета), для нахождения необходимой суммы воспользуемся формулой (135) определения приведенной стоимости аннуитета. Так как  = 20 млн. руб., n = 5, m = 1 и r = 30%, то:
= 20 млн. руб., n = 5, m = 1 и r = 30%, то:
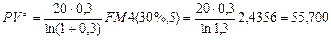 млн. руб.
млн. руб.
Таким образом, обладая 55,7 млн. руб., компания способна выполнить свои обязательства перед вкладчиками.
Пример 3.2.4. Имеется переменный аннуитет постнумерандо (тыс. руб.): 20, 12, 8, 45, 30. Рассчитайте: а) будущую стоимость аннуитета; б) приведенную стоимость аннуитетов, если его период совпадает с базовым периодом начисления процентов по сложной процентной ставке 25% годовых, т.е. равен одному году. Как изменятся полученные оценки, если исходный поток представляет собой аннуитет пренумерандо?
Решение. а) Обозначим (в тыс. руб.) С1 = 20, С2 = 12, С3 = 8, С4 = 45, С5 = 30 и r = 0,25. Изобразим схематично условие задачи на оси времени (одно деление равно одному году), помещая над осью члены аннуитета.





 20 12 8 45 30
20 12 8 45 30
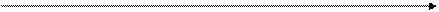 0 1 2 3 4 5 t лет
0 1 2 3 4 5 t лет
Для определения будущей стоимости аннуитета можно воспользоваться формулой (116). Для наглядности представим результаты расчетов в табличном виде.
(тыс. руб.)
| Год | Денежный поток | Множитель наращения при r = 25% | Наращенный поток |
| 2,4414 | 48,828 | ||
| 1,9531 | 23,4372 | ||
| 1,5625 | 12,5 | ||
| 1,25 | 56,25 | ||
| 171,0152 |
Из таблицы видно, что на первое денежное поступление в размере 20 тыс. руб. начисляются сложные проценты за 4 года и оно в конце пятого года станет равным 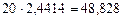 тыс. руб.; на второе денежное поступление в размере 12 тыс. руб начисляются сложные проценты за 3 года и оно в конце пятого года станет равным
тыс. руб.; на второе денежное поступление в размере 12 тыс. руб начисляются сложные проценты за 3 года и оно в конце пятого года станет равным 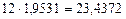 тыс. руб. и т.д. Будущая стоимость аннуитета равна сумме наращенных поступлений, т.е. стоимость аннуитета равна сумме наращенных поступлений, т.е.
тыс. руб. и т.д. Будущая стоимость аннуитета равна сумме наращенных поступлений, т.е. стоимость аннуитета равна сумме наращенных поступлений, т.е. 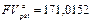 тыс. руб.
тыс. руб.
б) Для определения приведенной стоимости аннуитета можно воспользоваться формулой (117). Как и в предыдущем случае, для наглядности представим результаты расчетов в табличном виде:
(тыс. руб.)
| Год | Денежный поток | Дисконтный множитель при r = 25% | Приведенный поток |
| 0,8 | |||
| 0,64 | 7,68 | ||
| 0,512 | 4,096 | ||
| 0,4096 | 18,432 | ||
| 0,3277 | 9,831 | ||
| 56,039 |
Таким образом, с позиции начала первого года приведенная стоимость 20 тыс. руб. составляет 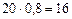 тыс. руб., приведенная стоимость 12 тыс. руб. составляет
тыс. руб., приведенная стоимость 12 тыс. руб. составляет 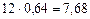 тыс. руб. и т.д. Суммируя приведенные стоимости всех денежных поступлений, получим приведенную стоимость аннуитета
тыс. руб. и т.д. Суммируя приведенные стоимости всех денежных поступлений, получим приведенную стоимость аннуитета 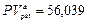 тыс. руб.
тыс. руб.
Конечно, при рассмотрении этого случая можно было вое пользоваться уже ранее найденной будущей стоимостью  , а именно:
, а именно:
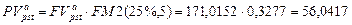 тыс. руб.
тыс. руб.
Расхождение в 2 руб. 70 коп. (0,0027 тыс. руб.) является следствием погрешности вычислений.
Если же исходный поток является аннуитетом пренумерандо, то схематично условие задачи выглядит таким образом:





 20 12 8 45 30
20 12 8 45 30
 0 1 2 3 4 5 t лет
0 1 2 3 4 5 t лет
Для определения будущей и приведенной стоимости этого аннуитета пренумерандо можно воспользоваться полученными результатами и формулами (118) и (119):
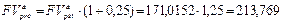 тыс. руб.;
тыс. руб.;
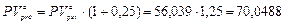 тыс. руб.
тыс. руб.
Пример 3.2.5. Согласно условиям финансового соглашения на счет в банке в течение 8 лет: а) в конце года; б) в начале года будут поступать денежные суммы, первая из которых равна 4 тыс. руб., а каждая следующая будет увеличиваться на 0,5 тыс. 1уб. Оцените этот аннуитет, если банк применяет процентную ставку 20% годовых и сложные проценты начисляются один раз в конце года. Как изменятся оценки аннуитета, если денежные суммы будут уменьшаться на 0,5 тыс. руб.?
Решение. а) Согласно условию имеем переменный аннуитет постнумерандо с постоянным абсолютным изменением его членов и, следовательно, для оценки аннуитета воспользуемся формулами (140) и (141). По условиям соглашения А = 4 тыс. руб., n = 8, r = 0,2, и если суммы возрастают, то z = 0,5 тыс. руб. Поэтому:
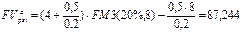 тыс. руб.;
тыс. руб.;
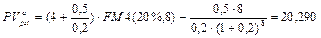 тыс. руб.
тыс. руб.
С целью проверки воспользуемся формулой (65):
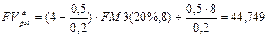 тыс. руб.,
тыс. руб.,
т.е. результаты вычислений совпадают с точностью до второго знака после запятой (отличие на 3 руб.).
Если суммы будут уменьшаться, то z = -0,5 и, следовательно,
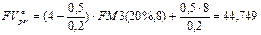 тыс. руб.
тыс. руб.
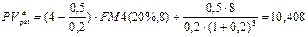 тыс. руб.
тыс. руб.
Заметим, что при z < 0 члены аннуитета убывают и число этих членов (равное числу периодов n) должно удовлетворять неравенству  , иначе можно получить отрицательные платежи, что лишено смысла, т.е. должно выполняться условие
, иначе можно получить отрицательные платежи, что лишено смысла, т.е. должно выполняться условие 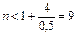 . Таким образом, в данной ситуации (при n = 8 ) все платежи положительны.
. Таким образом, в данной ситуации (при n = 8 ) все платежи положительны.
б) Оценки аннуитета пренумерандо нетрудно получить, используя соотношения 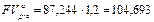 ,
, 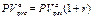 . Если z = 0,5, то
. Если z = 0,5, то
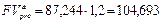 тыс. руб.;
тыс. руб.;
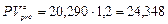 тыс. руб.
тыс. руб.
Если же z = -0,5, то
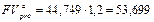 тыс. руб.;
тыс. руб.;
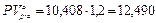 тыс. руб.
тыс. руб.
Нетрудно получить формулы оценки аннуитета, аналогичные формулам (140), (141), и для других ситуаций. Однако эти формулы приобретают несколько громоздкий вид. Например, если в переменном аннуитете постнумерандо с постоянным абсолютным изменением его членов начисление сложных процентов происходит m раз за период, то можно показать, что
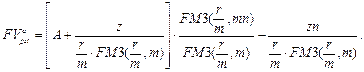
Так, если в условиях примера начисление сложных процентов происходит в конце каждого квартала (m = 4), то 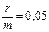 и z = 0,5 получаем:
и z = 0,5 получаем:
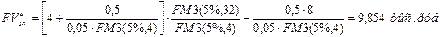
Пример 3.2.6. За 6 лет необходимо накопить 30 тыс. руб. Какой величины должен быть первый вклад, если предполагается каждый год увеличивать величину денежного поступления на 800 руб. и процентная ставка равна 25% годовых? Денежные поступления и начисление сложных процентов осуществляются в конце года. Определите, на какую величину необходимо увеличивать каждый год денежное поступление, если первый вклад будет равен 2 тыс. руб.
Решение. Полагая в формуле (140) 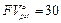 тыс. руб., z = 0,8 тыс. руб., п = 6 и r = 0,25 , получим уравнение:
тыс. руб., z = 0,8 тыс. руб., п = 6 и r = 0,25 , получим уравнение:
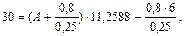
из которого находим размер первого вклада:
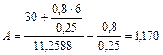 тыс. руб.
тыс. руб.
Если же известна величина первого вклада А = 2 тыс. руб. и неизвестна величина z абсолютного изменения денежных поступлений, то по формуле (140) получим:
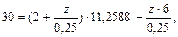
откуда:
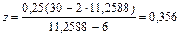 тыс. руб.
тыс. руб.
Пример 3.2.7. По условиям контракта на счет в банке поступают в течение 7 лет в конце года платежи. Первый платеж равен 4 тыс. руб., а каждый следующий по отношению к предыдущему увеличивается на 10%. Оцените этот аннуитет, если банк начисляет в конце каждого года сложные проценты из расчета 28% годовых.
Решение. Поскольку ежегодно платежи увеличиваются и 1,1 раза (на 10%), то денежный поток представляет собой переменный аннуитет постнумерандо с постоянным относительным изменением его членов. Поэтому для оценки аннуитета воспользуемся формулами (143) и (144). Полагая А = 4 тыс. руб., n = 7, r = 0,28 и q = 1,1, получим:
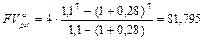 тыс. руб.;
тыс. руб.;
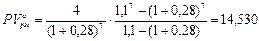 тыс. руб.
тыс. руб.
Пример 3.2.8. Компания за предыдущий год выплатила 2 тыс. руб. на акцию. Согласно прогнозам дивиденды по акциям этой компании будут расти на 100 руб. ежегодно в течение неопределенно долгого времени. Сделайте вывод о целесообразности покупки акций компании по цене 12 тыс. руб., если можно поместить деньги на депозит под 24% годовых. Изменится ли ситуация, если дивиденды по акциям будут расти на 8% ежегодно в течение неопределенно долгого времени?
Решение. Полагая А = 2 тыс. руб., z = 0,1 тыс. руб. и r = 0,24, по формуле (142) оценки бессрочного аннуитета найдем истинную стоимость акции:
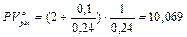 тыс. руб.
тыс. руб.
Так как истинная стоимость акции меньше ее цены, то не имеет смысла приобретать акцию.
Пусть теперь дивиденды по акциям растут на 8% в год, т.е. увеличиваются ежегодно в 1,08 раза. В этом случае истинная стоимость акции по формуле (145) при q = 1,08 составит:
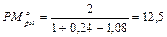 тыс. руб.
тыс. руб.
Таким образом, истинная стоимость акции больше ее цены, следовательно, имеет смысл ее приобретение.
Пример 3.2.9. Сдан участок в аренду на десять лет. Арендная плата будет осуществляться ежегодно по схеме постнумерандо на следующих условиях: в первые семь лет- по 20 тыс. руб., в оставшиеся три года - по 12 тыс. руб. Требуется оценить приведенную стоимость этого договора, если процентная ставка, используемая аналитиком, равна 22%.
Решение. Естественно, приведенная стоимость денежного потока должна оцениваться с позиции начала первого временного интервала. Решать данный пример можно различными способами в зависимости от того, какие аннуитеты будут выделены аналитиком. Во-первых, можно воспользоваться общей формулой (117). Представим еще три варианта решения.
а) Исходный поток можно представить как сумму двух аннуитетов: первый имеет А =12 тыс. руб. и продолжается десять лет; второй имеет А =8 тыс. руб. и продолжается первые семь лет. По формуле (121) можно оценить приведенную стоимость каждого аннуитета, а сумма этих оценок даст значение приведенной стоимости исходного денежного потока:

б) Исходный поток можно представить как разность двух аннуитетов: первый имеет А = 20 тыс. руб. и продолжается десять лет; второй имеет А = 8 и, начавшись в восьмом году, заканчивается в десятом. По формуле (121) можно оценить приведенную стоимость каждого аннуитета. Однако второй аннуитет в этом случае будет оценен с позиции начала восьмого года, поэтому полученную сумму необходимо дисконтировать с помощью формулы (65) к началу первого года. В этом случае оценки двух аннуитетов будут приведены к одному моменту времени, а их сумма даст оценку приведенной стоимости исходного денежного потока.

Исходный поток можно представить как сумму двух аннуитетов: первый имеет А = 20 тыс. руб. и продолжается семь лет; второй имеет А = 12 тыс. руб. и продолжается последние три года (т.е. является отсроченным аннуитетом). Поэтому по формулам (121) и (125) при h = 7, получим:

Дата добавления: 2020-10-25; просмотров: 603;











