Типовые примеры и методы их решения

Пример 2.4.1. Господин N собирается поместить на некоторый срок свободные денежные средства либо под сложную процентную ставку 30% годовых с ежеквартальным начислением процентов, либо под простую процентную ставку 48% годовых. Выясните, как выгоднее поступить при сроке: а) 3 года; б) 4 года?

Решение. а) Чтобы сделать правильный выбор, необходимо найти для данной сложной процентной ставки 30% эквивалентную простую процентную ставку и сравнить ее с предлагаемой простой процентной ставкой 48%. Используем формулу (81) при n = 3, m = 4 , r⁽⁴⁾ = 0,3:

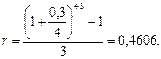
Так как r = 46,06% меньше 48%, то выгоднее на три года поместить капитал под простую процентную ставку 48%.

Конечно, можно было найти эквивалентную сложную процентную ставку для простой ставки 48% по формуле (82): 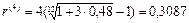и поскольку r⁽⁴⁾>30%, приходим, естественно, к такому же выводу.

б) Полагая n = 4 , m = 4, r⁽⁴⁾ = 0,3, по формуле (81) получим:

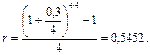
Так как r= 54,52% превышает 48%, то выгоднее на 4 года поместить капитал под сложную ставку.

Пример 2.4.2. Долговое обязательство учтено в банке за 9 месяцев до срока погашения по номинальной годовой учетной ставке d⁽⁴⁾ = 32% . По какой простой учетной ставке надо произвести учет этого обязательства, чтобы обеспечить банку тот же самый дисконт?

Решение. Полагая в формуле (83) n = 0,75, находим:

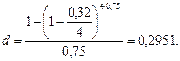
Таким образом, искомое значение простой учетной ставки составляет 29,51% годовых. С целью проверки можно воспользоваться формулой (84), где d = 0,2591 :

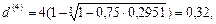или 32% .

Получив номинальную годовую учетную ставку, данную в условии примера, делаем вывод, что простая учетная ставка найдена верно.

Пример 2.4.3. Банком выдан кредит на три месяца под 27% годовых с ежемесячным начислением сложных процентов. Определите величину простой учетной ставки, обеспечивающей такую же величину начисленных процентов.

Решение. По формуле (87) при n = 0,25, r⁽¹²⁾ = 0,27 находим требуемую величину простой учетной ставки:

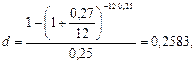или 25,83%.

Для проверки результата воспользуемся формулой (88):

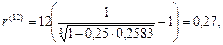
т.е. получили исходную сложную процентную ставку.

Пример 2.4.4. Определите сложную годовую учетную ставку с дисконтированием 2 раза в год, которая эквивалентна годовой номинальной процентной ставке 24%: а) с ежеквартальным начислением сложных процентов; б) с полугодовым начислением сложных процентов.

Решение.а) Применяем формулу (92) при m=2, l=4, r⁽⁴⁾=0,24:

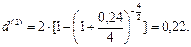
Проверим полученный ответ по формуле (91), где уже m=4, l=2:

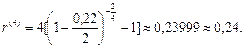
б) Из формулы (92) при m = l = 2 , r⁽²⁾ = 0,24 получим:

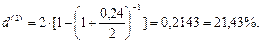
Заметим, что при m = l из формул (91) и (92) получим соответственно равенства:

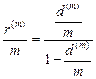и

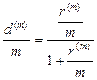
которые по существу являются иной записью равенств (3).

Пример 2.4.5. Определите величину силы роста при начислении непрерывных процентов в течение двух лет, которая эквивалентна: а) простой процентной ставке 26% годовых; б) сложной процентной ставке 26% годовых с ежемесячным начислением процентов.

Решение. а) Полагая в формуле (94) n = 2, r = 0,26 , находим:

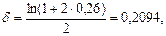или 20,94%. 2

Проверку полученного ответа можно осуществить по формуле (93):

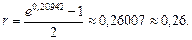
Из формулы (94) следует, что с ростом срока n величина эквивалентной непрерывной ставки будет уменьшаться. Например, при n = 10 лет сила роста 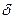= 12,81%; при n = 100 лет – 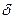= 3,3%

б) По формуле (97) при m = 12 , r⁽¹²⁾ = 0,26:

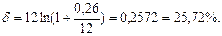
Для проверки воспользуемся формулой (98):

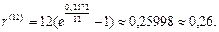
Заметим, что в отличие от предыдущего случая величина эквивалентной непрерывной ставки не зависит от величины срока, в течение которого происходит наращение.

Как видно из решения случая б), 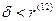. Вообще можно показать, что эквивалентные ставки r^(m), d^(l) и 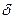при любых m и l удовлетворяют неравенствам: d^(l)< 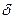<r^(m).

Пример 2.4.6. Банк предоставляет ссуду на 25 месяцев под 30% годовых с ежеквартальным начислением процентов по смешанной схеме. Определите эквивалентную годовую простую процентную ставку, обеспечивающую такой же доход банку от предоставления ссуды.

Решение. Покажем, что для данной ситуации нетрудно получить формулу в общем виде. Пусть в течение времени n используется сложная процентная ставка r^(m), но при начислении процентов применяется смешанная схема. Тогда по формуле (59) множитель наращения имеет вид 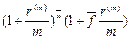, где 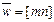(напомним, что квадратные скобки означают целую часть числа), 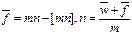. Множитель наращения при использовании простой процентной ставки согласно формуле (9) имеет вид 1 + nr. Приравнивая эти множители наращения, находим, что эквивалентная простая процентная ставка находится по формуле:

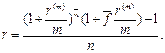
В нашем случае 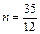года, m = 4, r⁽⁴⁾=0,3,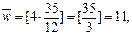 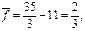поэтому:

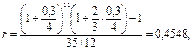
т.е. эквивалентная простая процентная ставка равна 45,48%.

Таким образом, из полученной выше формулы следует, что простая процентная ставка r эквивалентна по существу двум процентным ставкам: сложной ставке r(m), применяемой за время, равное целому числу подпериодов, и простой ставке r(m), применяемой за время, равное дробной части подпериода. При этом если дробная часть подпериода равна нулю ( 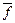= 0), то 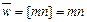и полученная выше формула совпадает с формулой (81), а если целое число подпериодов равно нулю ( 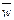= 0), то 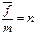и полученная формула примет вид r =r^(m).

Если бы начислялись только сложные проценты, то воспользовались бы формулой (81):

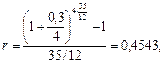
Пример 2.4.7. Банк принимает вклады до востребования под сложную процентную ставку 20% годовых при временной базе 365 дней. Какую простую годовую учетную ставку должен применить банк при учете векселя за 250 дней до срока его погашения, чтобы обеспечить себе такую же доходность, как и по вкладам до востребования? При учете используется временная база 360 дней.

Решение. Для определения эквивалентной простой годовой учетной ставки нельзя воспользоваться формулой (87), поскольку при ее выводе считалось, что временные базы ставок одинаковы. Однако необходимую для решения данного примера формулу нетрудно получить, приравнивая соответствующие множители наращения. Пусть T_d и T_r – временные базы соответственно учетной и процентной ставок, тогда из 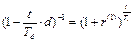получим:

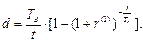
Таким образом, полагая r⁽¹⁾ = 0,2 , Т_r = 365 дней, Т_d = 360 дней, t = 250 дней, получим:

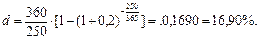
Кстати, если бы взяли одинаковую временную базу, то при Т_d = Т_r = 360 дней получили бы d = 17,13% , а при Т_d = Т_r = 365 дней – d = 17,14%.