Уравнение Эйлера. Теоретический и действительный напоры

Энергия, передаваемая жидкости или газу рабочим колесом центробежной машины, определяется в основ­ном значениями абсолютной, относительной и окружной скоростей на входе и выходе из межлопастных каналов. Параллелограммы этих скоростей даны на рис. 37, где обозначено: u -окружная скорость; w -относительная скорость, т. е. скорость потока относительно вращающе­гося колеса; с-абсолютная скорость, или скорость жидкости относительно неподвижного корпуса машин.

Характерными элементами являются также следую­щие углы: a -угол между векторами окружной и аб­солютной скоростей и b -угол, образованный вектором относительной и обратным направлением окружной ско­ростей; последнее определяется формой лопастей центро­бежной машины и режимом ее работы.

Элементы параллелограммов скоростей и геометри­ческие размеры колеса, относящиеся ко входу и выходу межлопастных каналов, отмечаются соответственно индексами 1 и 2.

В теории и расчетах центробежных машин использу­ют также окружную и радиальную составляющие абсо­лютных и относительных скоростей, обозначаемые индек­сами uиr. Например, 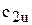-окружная проекция абсо­лютной скорости на выходе из рабочего колеса.

Применим к потоку, проходящему через рабочее ко­лесо машины, уравнение моментов количества движения предполагая, что поток, проходящий через межлопастные каналы, -плоский, т. е. определяющийся только двумя компонентами: 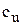,и .

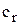Кроме того, будем предполагать, что влияние рабочих лопастей на поток столь существенно, что скорости во всех точках цилиндрических сечений постоянного радиуса сохраняются постоянными. Это возможно только при очень большом (условно – бесконечном) количестве тонких лопастей.

Рис. 37. Разрезы колеса центробежной машины. Параллелограммы скоростей на входе и выходе межлопастных каналов

Поэтому в литературе величины, ха­рактеризующие поток через межлопастные каналы при указанном предположении, условно обозначают индек­сом ¥ и называют параметрами при бесконечном коли­честве лопастей.

Если колесо пропускает расход Q жидкости или газа с плотностью r, то моменты секундных количеств дви­жения на входе и выходе из межлопастных каналов в соответствии с рис. 37 будут:

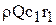и .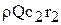

Импульс внешнего момента, действующего на массу жидкости, проходящей через колесо, равен изменению момента количества движения этой массы, поэтому

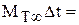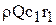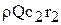( - )Dt, (35)

где 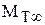- теоретический момент, прилагаемый к потоку в межлопастных каналах, при бесконечном количестве лопастей.

Момент, подводимый к валу машины, больше 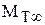вследствие механического трения в подшипниках и уплотнениях вала и гидравлического (газового) трения нерабочей стороны колес о жидкость (газ).

Введем в уравнение (35) конструктивные радиусы, имея в виду, что 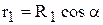и 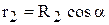, тогда

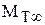= rQ( .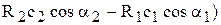

Из рис. 3-2 следует:

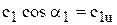и .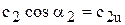

Поэтому

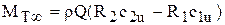. (36)

Мощность, передаваемая потоку в межлопастных каналах,

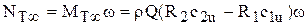
или

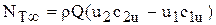. (37)

Если обозначить величину удельной теоретической энергии 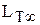(без учета потерь энергии в проточной части колеса), то теоретическая мощность 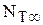насоса будет:

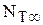= rQ 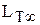. (38)

Сопоставляя (37) и (38), получаем:

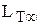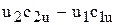= . (39)

Удельная работа и напор связаны зависимостью 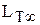= 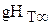. Следовательно, из (39)

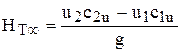, (40)

где 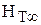- теоретический напор колеса центробежного на­соса, м, при бесконечном количестве лопастей.

Уравнения (36), (37) и (39) являются основными уравнениями центробежных машин.

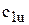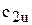При расчете момента, мощности и напора по фор­мулам (36), (37) и (39) следует иметь в виду, что скорости и постоянны соответственно по окруж­ностям радиусов 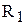и .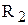

Следует отметить, что в действительных условиях на­блюдается некоторая неравномерность распределения абсолютных и относительных скоростей как на входе, так и на выходе из рабочего колеса.

Уравнение Эйлера можно представить в другом виде, воспользовавшись параллелограммами скоростей на вхо­де и выходе:

;

.

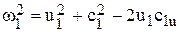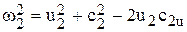Определив отсюда произведения 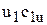и 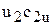и под­ставив их в уравнение (40), получим:

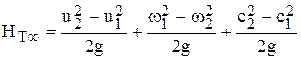. (41)

Физическая величина 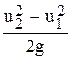представ­ляет собой напор, обусловленный работой центробежной силы жидкости.

Действительно, величина центробежной силы жидко­сти 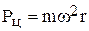или для 1 кг жидкости .

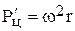Работа силы 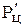на элементарном пути dr:

.

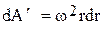Работа силы Р'_ц на пути от входа в межлопастные каналы до выхода из них

.

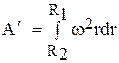При w = const

.

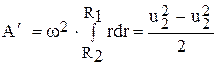Напор, соответствующий 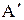, будет .

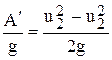Члены уравнения (41) 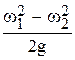и 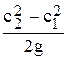выражают соответственно прирост напора за счет преобразования кинетических энергий относительного и абсолютного дви­жений.

Так как с₁ и с₂есть абсолютные скорости на входе и выходе межлопастных каналов, то 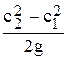- скоростной напор, создаваемый лопастями рабочего колеса:

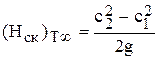. (42)

Поэтому теоретический статический напор (удельная потенциальная энергия):

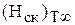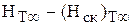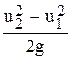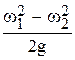= = + . (43)

В большинстве случаев поток, входящий в межло­пастные каналы, приведен во вращательное движение благодаря непосредственному соприкосновению с валом и втулкой колеса и вследствие импульсивного обмена между массами жидкости (газа), уже вошедшими в межлопастные каналы, и массами, находящимися еще вне их. Это явление называют закручиванием потока на входе. Интенсивность закручивания потока на входе ха­рактеризуется величиной 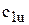(м/с), или в относительных единицах, .

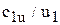Из уравнения Эйлера (40) следует, что теоретиче­ский напор Н_т зависит от окружной проекции скорости на входе в межлопастные каналы 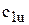. Однако сказанное справедливо только в том случае, если закручивание по­тока перед колесом вызвано специальными направляю­щими аппаратами. Если же закручивание потока вызва­но воздействием самого рабочего колеса, то оно сопро­вождается увеличением теоретического напора.

,

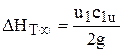Поэтому при закручивании потока самим рабочим колесом

.

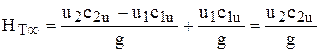Следовательно, при определении теоретических ха­рактеристик машины без входного направляющего устройства (или входного патрубка специальной формы, обеспечивающей закручивание потока перед рабочим колесом) основные уравнения представляются в виде:

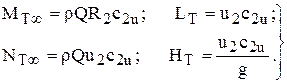(44)

Это - уравнения центробежной машины с радиаль­ным входом в межлопастные каналы.

Если 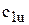=0, то из треугольника скоростей на входе следует:

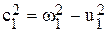
Поэтому из уравнения (41) для этого случая получим:

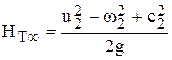; (45)

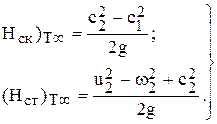(46)

Действительный напор, создаваемый колесом, меньше теоретического при бесконечном количестве лопастей H < 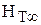. Во-первых, это объясняется тем, что часть энергии, получаемой жидкостью в рабочем колесе, за­трачивается на преодоление гидравлических сопротив­лений в проточной части машины. Эти потери учитыва­ются гидравлическим к. п. д. 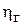. Во-вторых, указанное неравенство обусловлено отклонением действительной картины течения от предполагаемой струйной при беско­нечном количестве лопастей.

Это учитывается введением поправочного коэффици­ента m на конечное количество лопастей

.

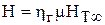Гидравлический к. п. д. современных центробежных машин оценивает гидравлическое совершенство проточ­ной части их и лежит в пределах 0,80-0,96.

Поправочный коэффициент m<1 определяется по по­луэмпирическим формулам Стодолы и Пфлейдерера.

По методу Стодолы

.

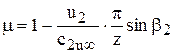Эта формула хорошо согласуется с практикой.

,

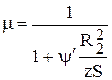где 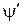-опытный коэффициент, зависящий от 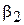; S - статический момент средней линии тока по лопасти.