Приведение сил и моментов к входному

Звену механизма

Анализ движения машинного агрегата с помощью динамической модели сводится к динамике тела с переменным моментом инерции и вращающимся вокруг неподвижной оси под действием движущихся сил и сил полезного сопротивления. При выполнении динамического анализа всеми силами, величина которых составляет не более 5% от наибольшего значения сил полезного сопротивления в заданном положении механизма, пренебрегают.

Приведение сил осуществляется на основании равенства работ (мощностей), развиваемых силами, приложенными к динамической модели и к реальному машинному агрегату.

В общем виде момент сил, приведенный к кривошипному валу, определяется из равенства потока энергии динамической модели и машинного агрегата

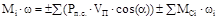, (5.8)

где w_i – угловая скорость динамической модели (см.рис.5.1);

M_i – момент сил, приведенный к динамической модели;

M_i × w – мощность, развиваемая приведенным моментом;

P_п.с – cила полезного сопротивления;

V_п– скорость точки приложения этой силы;

a – угол между вектором силы Р_пс и вектором скорости V_п (в реальных рабочих машинах чаще всего α=180⁰);

M_ci – момент сил сопротивления, приложенный к i-му звену механизма;

w_i – угловая скорость i-го звена в данном положении механизма;

P_п.с.V_п cos(α) – мощность, развиваемая действующими в механизме силами и моментами.

Решая уравнение (5.8) относительно М_пр, получим:

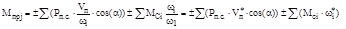, (5.9)

где V_п^*=V_П / ω_i – аналог скорости точки приложения силы полезного сопротивления;

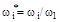– аналог угловой скорости i-го звена механизма.

Анализ зависимости (5.9) показывает, что приведенный момент не зависит от величины и направления угловой скорости динамической модели, а зависит только от отношения угловых и линейных скоростей, т.е. от аналогов линейных и угловых скоростей звеньев, которые изменяются только с изменением положения механизма. Приведенные моменты сил движущих – положительные, а сил сопротивления – отрицательные.

Приведение масс

В основу приведения масс положено условие равенства кинетической энергии механизма и динамической модели. В этом случае закон движения динамической модели будет таким же, как и закон движения звена приведения реального механизма. Величину приведенного момента инерции I_пр всего механизма найдем как сумму приведенных моментов инерции всех звеньев.

Для определения величины приведенного момента инерции каждого звена механизма необходимо приравнять кинетическую энергию рассматриваемого звена к кинетической энергии этого же звена, но приведенную к динамической модели. Приняв в качестве динамической модели кривошипный вал, который вращается с угловой скоростью ω_i, то его кинетическая энергия равна

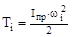. (5.10)

В зависимости от характера движения звена существуют следующие варианты определения кинетической энергии и приведенного момента инерции:

а) при поступательном движении i-го звена механизма

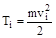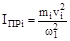; ; (5.11)

б) при вращательном движении i-го звена вокруг неподвижной оси, проходящей через центр масс этого звена,

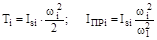; (5.12)

в) при плоскопараллельном движении i-го звена или при вращательном движении звена вокруг оси, не проходящей через центр масс,

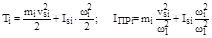, (5.13)

где m_i– масса i-го звена;

v _si– скорость центра масс i-го звена;

I_si– момент инерции i-го звена относительно оси, проходящей через центр масс;

w_i – угловая скорость i-го звена.

Приравняв кинетическую энергию динамической модели (5.10) к сумме кинетических энергий всех звеньев (5.11–5.13), получим зависимость для определения приведенного момента инерции в j-м его положении

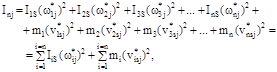(5.14)

где 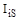– момент инерции i-го звена относительно оси, проходящей через центр масс S, определяется по исходным данным; для конкретного звена (I_is = const);

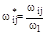– аналог угловой скорости i-го звена в j-м положении механизма; принимается по результатам построения планов скоростей;

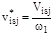– аналог скорости центра масс i-го звена в j-м положении механизма; принимается по результатам построения планов скоростей, м;

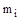– масса i-го звена; определяется по исходным данным.

Когда все звенья заменены одним звеном, обладающим приведенным моментом инерции I_пр, и все реально действующие силы и моменты, приложенные к различным звеньям механизма, заменены одним приведенным моментом М_пр, можно рассматривать движение только одного замещающего звена, вращающегося с угловой скоростью w₁ вокруг неподвижной оси.