Определение момента инерции маховика

На протяжении цикла работы машинного агрегата, вследствие неравенства работ движущих сил и сил сопротивлений, а также периодических изменений приведенного момента инерции, кривошипный вал будет вращаться с переменной угловой скоростью w₁, изменяющейся по некоторому периодическому закону. В течение цикла w₁ она колеблется относительно постоянного среднего значения w_ср в пределах от w_min до w_max.

Колебания скорости во время установившегося движения могут достигать такой величины, которая не будет допустимой по условию качественного выполнения технологического процесса. В таких случаях возникает вопрос о регулировании в заранее заданных пределах величин этих колебаний. Регулировка периодических колебаний скоростей при установившемся движении осуществляется подбором массы маховика.

Изменение угловой скорости в пределах от w_min до w_max в соответствии с теоремой об изменении кинетической энергии обусловлено разностью работ движущих сил и сил полезного сопротивления:

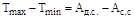, (5.15)

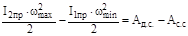, (5.16)

где 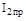– значение приведенного момента в положении механизма, где w₁ = w_max;

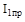– значение приведенного момента в положении механизма, где w₁ = w_min;

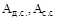– работа, выполненная движущими силами и силами сопротивления при перемещении механизма с положения, где w₁ = w_max, до положения, где w₁= w_min.

Обозначая

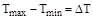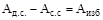и , (5.17)

зависимость (5.17) примет следующий вид:

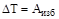. (5.18)

Зависимость (5.18) показывает, что при изменении угловой скорости от w_min до w_max изменение кинетической энергии всего механизма (вместе с маховиком) равно избыточной работе.

Звенья механизма могут быть разделены на две группы. В первую группу входит звено приведения, на котором обычно размещается маховик, а также все звенья, связанные со звеном приведения постоянным передаточным отношением. Приведенный момент инерции звеньев этой группы постоянен и не зависит от положения механизма. При наличии в механизме маховика его кинетическая энергия обычно составляет 90–95% от кинетической энергии звеньев этой группы. Поэтому в первом приближении можно считать, что кинетическая энергия звеньев первой группы равна кинетической энергии маховика, т.е. предложить

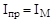. (5.19)

Ко второй группе относятся все остальные звенья механизма. Приведенные моменты инерции звеньев этой группы переменны, они зависят от положения механизма. Обозначим их сумму I_зв. С учетом принятых обозначений формула (5.19) примет вид

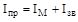. (5.20)

С учетом равенства (5.15) зависимость (5.20) примет следующий вид:

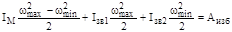. (5.21)

Выражение

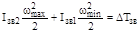(5.22)

представляет изменение кинетической энергии звеньев механизма без маховика при изменении угловой скорости от w_min до w_max, а выражение 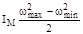представляет изменение кинетической энергии маховика при изменении угловой скорости от w_min до w_max. С учетом формулы (5.20) зависимость (5.21) примет следующий вид:

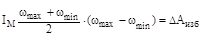. (5.23)

Обозначив в формуле (5.23) выражение

, ,

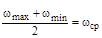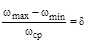получим

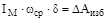, (5.24)

где δ – коэффициент неравномерности хода машинного агрегата;

w_ср – средняя скорость звена приведения.

Решая это уравнение относительно I_м, получим формулу для определения момента инерции маховика:

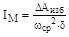. (5.25)

Подбирая величину маховой массы, обладающей необходимым моментом инерции, мы можем ограничить размах колебаний угловой скорости w₁ таким образом, что коэффициент неравномерности δ будет иметь заданное значение. Следовательно, задача данной части курсового проекта состоит в расчете момента инерции маховика по формуле (5.25) с учетом заданного значения δ и w_ср и в определении размеров маховика.

Существует несколько методов определения момента инерции маховика. Студентам рекомендуется произвести расчет маховика по методу Н.И. Мерцалова или по методу проф. Ф. Виттенбауэра – построение диаграммы энергомасс.