Производственные функции с постоянными пропорциями
Рассмотрим, что произойдет с производственной функцией (7) в том случае, когда параметр ρ стремится к своему другому пределу, т. е. ρ →∞.
Очевидно, что, согласно (15), в этом случае ρ → 0, т. е. эластичность замещения также стремится к своему другому крайнему значению.
Построим функцию
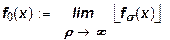
где 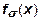 - (7) .
- (7) . 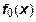 - искомая функция, где индекс 0 - подчеркивает равенство нулю ее эластичности замещения.
- искомая функция, где индекс 0 - подчеркивает равенство нулю ее эластичности замещения.
При δ = 1 для случая двух производственных ресурсов, т. е. х = (x1,x2)
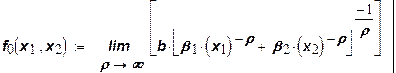
После преобразования получим: при 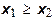 ,
, 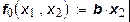 ;
;
при 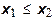 ,
, 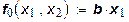 .
.
В целом функция f0(x1,x2)может быть представлена в виде:
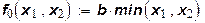 . (16)
. (16)
Для функции (16) построим соответствующую ей функцию 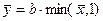 (рис. 4).
(рис. 4).
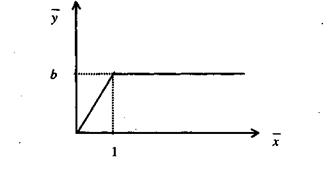
Рис. 4
Эта функция имеет излом в точке х = 1, т. е. для функции не выполняете предположение о дифференцируемости при всех положительных значениях переменных. Рассмотрим изокванты функции (16). Уравнение изоквант имеет вид:
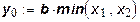
Из этого соотношения следует, что для выпуска продукции в объеме, равном у0,достаточно использовать ресурсы в объеме:
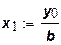 ,
, 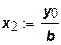 .
.
Увеличение количества одного из ресурсов сверх этой величины без изменения количества другого приводит к выпуску того же самого объема продукции у0, поэтому изокванты имеют вид, показанный на рис. 5.
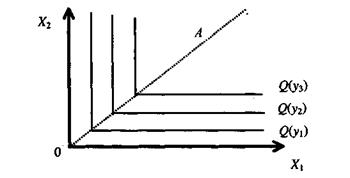
Рис. 5
В точках, лежащих на луче ОА, на котором выполнено условие 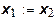 , находятся изломы изоквант. Особенностью полученной функции является наличие рациональных пропорций между ресурсами, задаваемыми соотношением
, находятся изломы изоквант. Особенностью полученной функции является наличие рациональных пропорций между ресурсами, задаваемыми соотношением 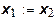 . Когда количество одного ресурса превышает количество другого, избыток ресурсов пользы принести не может. Таким образом, замена одного ресурса другим здесь отсутствует. Производственные функции такого типа принято называть производственными функциями с постоянными пропорциями. Они имеют вид:
. Когда количество одного ресурса превышает количество другого, избыток ресурсов пользы принести не может. Таким образом, замена одного ресурса другим здесь отсутствует. Производственные функции такого типа принято называть производственными функциями с постоянными пропорциями. Они имеют вид:
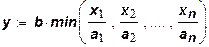 (17)
(17)
где 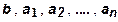 - положительные параметры.
- положительные параметры.
Функция характеризуется постоянной отдачей от расширения масштабов производства. Предельная норма замещения γ при х1 > х2равна -∞, а при х1 < х2 равна 0.
Функция имеет нулевую эластичность замещения. Функция предназначена для моделирования строго определенных технологий, не допускающих отклонений от норм используемых ресурсов и от технологических норм использования ресурсов на единицу продукции.
Дата добавления: 2020-10-25; просмотров: 521;











