Нелинейные статические модели

Пусть 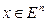. Рассмотрим представление линейной модели в виде (4). Вместо линейных связей 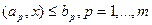на переменные модели наложим нелинейные связи:

g_p(x) ≤ 0,р = 1,...,т. (8)

Модель (8) – общее представление нелинейной статической модели с конечным числом ограничений.

Так же как и в случае линейных систем, модель (8) можно представить в виде (7), только теперь множество X уже не является многогранным.

Среди нелинейных статических моделей, используемых в экономико-математических моделях, наиболее важную роль играют модели, для которых множество допустимых значений Xявляется выпуклым, точнее говоря, вместе с любыми двумя векторами 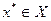и этому множеству принадлежит весь отрезок, равный

х = ах^*+ (1 - а) х^**, где а ∈ (0; 1).

Для рассмотренных линейных статических моделей множество X всегда выпукло. Для нелинейных моделей это не всегда так. Модели с выпуклым множеством X более удобны для исследования, поэтому модель стараются сформулировать так, чтобы множество X было выпукло.

Рассмотрим вопрос об условиях, достаточных для того, чтобы множество допустимых значений X, описываемое соотношением (8), было выпуклым. Этот вопрос решается на основе введения понятия выпуклой функции. Функция g(х), где 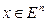, называется выпуклой вниз, если для любых значений х^* и х^** и при любом числе а, изменяющимся от 0 до 1, выполнено неравенство:

g(ax^*+ (1 - a)x^**) ≤ ag(x^*) + (1 - a)g(x^**). (9)

Если же для некоторой функции выполнено обратное условие, то ее называют вогнутой (или выпуклой вниз). В том случае, когда все нелинейные функции g_p(x), (р = 1,..., т) выпуклы, множество х тоже выпукло. Понятие выпуклости функции играет важную роль в экономико-математическом моделировании, поскольку позволяет получить интересные качественные результаты.

Как в линейных, так и в нелинейных экономико-математических моделях множество X обычно содержит более одного допустимого вектора. Это означает, что имеется некоторая свобода выбора: соотношение модели не определяет единственным образом то, что произойдет с изучаемой экономической системой. Это позволяет ввести понятие внешнего воздействия или управления, определяющего судьбу моделируемой системы.

В статических моделях типа (3) или (8) управлением является вектор x ∈ Еⁿ, причем необходимо выбирать такие его значения, которые удовлетворяют всем ограничениям (3) или (8).

При исследовании некоторых моделей типа (3) или (8) фактически надо выбирать не nзначений переменных, а меньшее число. Например, если в системе (3) часть неравенств объединяется в равенство (1), то, разрешив эту систему равенств, часть переменных можно выразить через другие, т. е. представить модель (3) в виде:

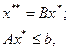(10)

где А и В – матрицы, а b – вектор. Тогда управлениями будут переменные, вошедшие в вектор х^*, а переменные из вектора х^** будут определяться внутри модели.

Представление моделей вида (3) или (5) в виде (10) позволяет ввести понятие экзогенных и эндогенных переменных. В модели (10) экзогенными (т. е. происходящими извне) являются переменные, составляющие вектор х^*, эндогенными - переменные, вошедшие в вектор х^**.