Методологические основы экономико-математического моделирования

Экономическая наука включает в себя - как необходимые инструментальные средства - математические методы и модели. Их использование позволяет формализовать важнейшие связи экономических систем и на этой основе производить анализ экономических систем, осуществлять прогнозирование и оптимизацию. Математические и эконометрические методы позволяют получать новые знания о неэкономическом объекте и его поведении, оценивать форму и параметры зависимостей его переменных.

Любое экономическое исследование всегда предполагает объединение теории (математической модели) с практикой (экспериментом и статистическими иными). Примерами экономических моделей являются модели предприятия, модели конкурентного равновесия на товарных и финансовых рынках, модели экономического роста и многие другие.

Формализация основных особенностей функционирования экономических объектов позволяет оценить возможные последствия и использовать такие оценки в управлении.

Модель – это материальный или мысленно представляемый объект, который в процессе исследования замещает объект-оригинал, так что его непосредственное: изучение дает новые знания об объекте-оригинале.

Под моделированием понимают процесс построения, изучения и применения моделей. Оно является методом познания с помощью объектов-заместителей. Необходимость использования этого метода определяется тем, что многие объекты или проблемы непосредственно исследовать или совсем невозможно, когда объект недосягаем либо реально не существует (будущее состояние экономики), или же это исследование требует много времени и средств.

Основным способом моделирования в экономике является метод математического моделирования, который представляет собой описание основных особенностей реального процесса с помощью системы математических формул. Математическая модель объекта, процесса или явления, как определенная математическая задача, включает две группы элементов:

· характеристики объектов, которые нужно определить (неизвестные вели­чины), - компоненты вектора Y = (у_i));

· характеристики внешних (по отношению к моделируемому объекту) изменяющихся условий - компоненты вектора X - (х_i).

Моделируемая задача может также включать совокупность внутренних параметров объектов А. Условия и параметры, описываемые X и А, рассматриваются как экзогенные, определяемые вне модели, а величины, составляющие век-I Р К, - как эндогенные, определенные с помощью модели.

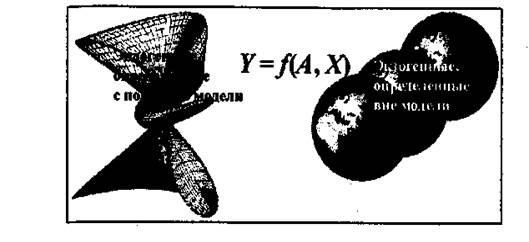Рис. 1

Математическую модель можно интерпретировать как особый преобразователь внешних условий объекта («входа») X в искомой характеристике объекта («выхода») Y.

По способам выражения соотношений между внешними условиями, внутренними параметрами и искомыми характеристиками математические модели делятся на два основных типа: функциональные и структурные.

Основная идея функциональных моделей – познание сущности объекта через важнейшие проявления этой сущности: деятельности, функционирования, поведения. Внутренняя структура при этом не изучается, а информация о структуре не используется. Функциональная модель имитирует поведение объекта так, что задавая значения «входа» X, можно получать значения «выхода» Y. Построить функциональную модель – значит отыскать оператор D, связывающий Xи Y:

Y = D(X).

Структурные модели отражают внутреннюю организацию объекта: его составные части, внутренние параметры и их связи с «входом» и «выходом».

Наиболее распространены два вида структурной модели:

· все неизвестные выражаются в виде функции от внешних условий и внутренних условий объекта:

;

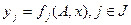· неизвестные определяются совместно, на основе системы отношений этого вида, т. е. уравнений, неравенств и т. д.:

.

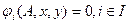Функциональные и структурные модели дополняют друг друга. С одной стороны, при изучении функциональных моделей возникают гипотезы о внутренней структуре объекта, объясняющей его функционирование, и тем самым открывается путь для структурного моделирования. С другой стороны, анализ структурных моделей дает ценную информацию о том, как объект реагирует на изменение внешних условий.

По степени сложности математические модели экономических объектов и явлений подразделяются на несколько основных типов.

К первому типу относятся функциональные модели, которые выражают прямые зависимости между известными (экзогенными) или неизвестными (эндогенными) величинами. Необходимые для построения модели параметры определяются на основе нормативных данных или статистическим способом.

Модели второго типа – это модели, выраженные с помощью систем уравнений относительно эндогенных величин. Они выражают обычно балансовое соотношение между различными экономическими показателями и используются для нахождения сбалансированных плановых решений (например, модель межотраслевого баланса).

Третья группа - модели оптимизационного типа. Основную часть такой модели составляют системы уравнений или неравенств относительно эндогенных величин. При этом необходимо найти такое решение этой системы, которое давало бы оптимальное (т. е. максимальное или минимальное в зависимости от постановки задачи) значение некоторого экономического показателя. Основными моделями этого типа, применяемыми в планировании, являются задачи линейного программирования.

К четвертой группе относятся имитационные модели, которые используются в составе человеко-машинных или игровых имитационных систем.

Пятую группу составляют более сложные образования – такие, как системы и комплексы взаимосвязанных моделей, относящихся к перечисленным выше типам.

Развитие систем моделей позволяет точнее отразить самые различные аспекты планирования и функционирования экономических объектов, в частности, находить оптимальные решения, сочетающие рациональное соотношение между отраслевым и региональным аспектами планирования и управления.