Линейные статические модели

В них рассматривается конечное число переменных – n. Переменные модели мы обозначим как х₁, х₂,... х_n. Предполагается, что эти переменные принимают вещественные значения. Связи в линейной модели в соответствии с ее названием имеют вид системы линейных равенств и неравенств.

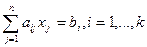; (1)

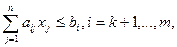(2)

где а_ij,и b_i – заданные числа.

Каждое равенство системы (1) можно представить в виде неравенств, т. е. система эквивалентна совокупности неравенств:

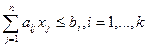
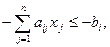
Поэтому линейную систему часто представляют в виде:

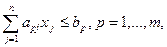(3)

Здесь числа а_p и b_p не совпадают с коэффициентами систем (1) и (2).

Модели типа (3) наиболее простые среди экономико-математических моделей. Часто их записывают в сокращенном векторном виде. Для этого вместо n переменных в модели используют единственную – вектор х, имеющий n составляющих:

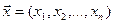
Чтобы подчеркнуть векторную природу переменной 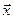, применяют запись вида 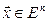, где 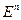– n-мерное евклидово пространство. Принадлежность вектора 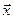пространству 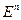означает, что вектор 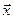имеет n вещественных составляющих x_j, причем векторы 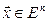и 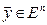, можно складывать по правилу: 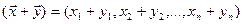, и умножать на вещественное число λ: 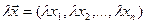. Кроме того, определено произведение двух векторов: .

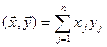На основе понятия скалярного произведения модель (3) можно представить в сокращенном виде:

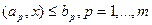, (4)

где а_р = (а_р1 , а_р2,. . . , а_рт) ∈ Еⁿ – векторы, состоящие из коэффициентов системы (3).

Обычно векторная запись имеет еще более сокращенный вид. Для этого из коэффициентов a_pj системы (3) образуют прямоугольную матрицу:

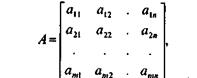
а из коэффициентов b_р составляют вектор 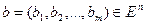. Тогда соотношение (3) переписывается в виде:

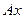≦b. (5)

В записи (5) использован знак неравенства ≦ . Для двух векторов а и b, принадлежащих пространству Еⁿ, запись а ≦ bозначает, что выполняются неравенства

a_i ≤b_i,i=1,...,m, (6)

причем все они могут одновременно быть равенствами. Запись ≤ для векторов означает, что все неравенства (6) одновременно в равенство обращаться не должны.

Множество допустимых значений переменной х, которое мы обозначим рез X, для модели (3) является многогранным. Можно сказать, что рассматриваемые линейные статические модели имеют общий вид:

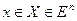, (7)

где X – многогранное множество.

Для того чтобы описать конкретное множество X, его представляют в одном из видов (3), (4) или (5).