Модель общего равновесия Вальраса

В общем случае, спрос на товар является функцией цен всех других товаров, дохода и количества потребителей. При данном доходе и количестве потребителей функция спроса на товар является функцией цен всех т товаров:

Q^D_i=D_i(P₁,...,P_i,...,P_m)_, i=1,2,...,т. (5.17)

На совершенно конкурентном рынке предложение товара также является функцией цен всех т товаров:

Q^S_i=S_i(P₁,...,P_i,...,P_m), i = 1,2,.:,m. (5.18)

Тогда функция избыточного спроса(ED; excess demand — англ.) на товар может быть представлена как разность между функцией спроса и функцией предложения. Обозначим избыточный спрос на i-й товар EDi тогда

ED_i(P₁,…P_i,…P_m)= D_i(P₁,...P_,i...P_m)-S_i(P_l,...,P_i,...,P_m). (5.19)

Кривая избыточного спроса может быть построена посредством горизонтального вычитаниякривой предложения из кривой спроса (рис. 5.7).

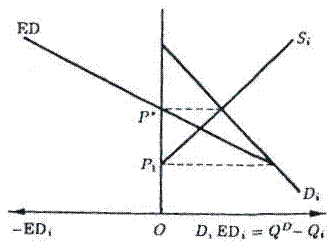
Рис. 5.7. Кривая избыточного спроса

Функция избыточного спроса позволяет рассматривать предложение как отрицательный избыток спроса, а спрос — как положительный его избыток. Так, на рис. 5.7 участок кривой избыточного спроса, ED, левее оси цены характеризует величину отрицательного спроса, т. е. предложения, а правее — ее величину положительного спроса. В этой модели различие между спросом и предложением исчезает. Поэтому в число т товаров в функцию избыточного спроса можно включить не только все конечные товары, но и все факторы производства, а также и все другие товары вплоть до невоспроизводимых (например, предметы антиквариата). Тогда условием равновесия становится равенство избыточного спроса нулю:

ED_i (P₁,...,P_m) = 0. (5.20)

Переходя к общему равновесию, мы получим систему, содержащую т уравнений вида для т товаров. Однако не все эти уравнения являются независимыми. Для экономики в целом общая ценность покупок всегда равна общей ценности продаж, и, значит,

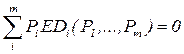(5.21)

Равенство (5.21) интерпретируют обычно как закон Вальраса. Он утверждает, что если все рынки, кроме одного, т. е. т-1 рынков, находятся в равновесии, то и оставшийся (т-1)-й рынок также находится в равновесии. А это значит, что число независимых уравнений в системе равно т - 1.

В принципе решить систему, состоящую из т – 1 независимых уравнений, относительно т переменных невозможно. Однако число последних можно уменьшить на единицу, выбрав один товар в качестве единицы счета (фр. numeraire) и разделив все цены на Р₁. Тогда (5.21) примет вид

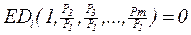. (5.22)

Таким образом, мы получили систему, состоящую из т – 1 уравнения, допускающую единственное решение относительно (т - 1 )-й цены.

При функциях спроса и предложения

Q^D =A-aP и Q^S =В + bР

функцией избыточного спроса будет

Е_Q =(А-В)-(а + b)Р.

Для рынка двух товаров условие (5.20) имеет вид:

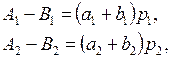
откуда, разделив первое уравнение на второе, получим

.

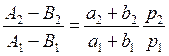Приняв цену первого товара в качестве единицы счета, обозначим

.

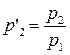Поэтому можно записать уравнение Вальраса (5.22):

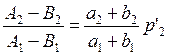(5.23)

Условие «расчистки рынка» (5.21) имеет следующий вид:

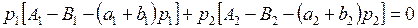. (5.24)

Уравнения (5.23), (5.24) позволяют найти искомые цены товаров.

В принципе, система уравнений Вальраса имеет решение, если количество независимых уравнений равно числу неизвестных в системе. Однако равенство количества независимых уравнений числу неизвестных — это необходимое, но не достаточное условие решения системы уравнений общего равновесия.

Существование равновесия зависит от того, обеспечивает ли поведение субъектов рынка пересечение кривых спроса и предложения при положительной цене, его стабильность зависит от соотношения наклонов кривых спроса и предложения (наклон кривой спроса меньше наклона кривой предложения), а его единственность связана с наклоном кривой избыточного спроса, характеризующей разность между объемами спроса и предложения или любой положительной цене.