Простой обмен в двухсубъектной двухпродуктовой экономике
Представим себе экономику, в которой нет производства, состоящую из двух субъектов, А и В, изначальноимеющих два товара, X и Y, в количествах (Х0А, Y0A) и соответственно (Х0В, Y0В). Определим равновесное состояние, то есть такие количества товаров, при которых обмен между субъектами прекратится.
| Кривая предложения из запаса |
Проанализируем влияние изменения цен товаров на эффект замены в товарном наборе потребителя. Бюджетное уравнение для одного из субъектов может быть представлено и в виде
 , (5.1)
, (5.1)
где I можно интерпретировать как бюджет субъекта А; px и py – цены (идеальные) товаров.
При изменении цен (например, снижении цены товара X) изменится наклон бюджетной линии. Рассмотрим, как при этом будет изменяться наклон бюджетных линий, проходящих через точку начального набора товаров SA, то есть обеспечивающих ту же покупательную способность (рис. 5.2).

|
| Х0А Х1А X Х1В Х1В Рис. 5.2. Кривые предложения двух субъектов |
На рис. 5.2а, представлено семейство кривых безразличия субъекта A (U0A, ..., U3A). Начальное наличие благ представлено точкой SA, лежащей на низшей кривой безразличия U0A.
Оптимум субъекта А определяется точкой касания бюджетной линии I0А и кривой безразличия U0А в точке SA. В этом случае он откажется от обмена со вторым субъектом. Если относительная цена товара X окажется ниже, так что соотношение цен X и Y будет отображаться бюджетной линии I1А (вместо I0А), касающейся более высокой кривой безразличия U1А в точке А, наш субъект согласится обменять Y0АY1А единиц товара Y на X0АX1А товара X. Если цена X относительно цены Y будет и далее снижаться, так что бюджетная линия будет и дальше поворачиваться вокруг точки SA от I1А до I3А, субъект А сможет достигать все более высоких кривых безразличия.
Кривая предложения ОСA товара Y из его начального запаса Y0А к обмену на товар X (ОС; offer curve — англ.)представляет собой множество точек (SA, А, B, С, ...) касания кривых безразличия и бюджетных линий, проходящих через точку начального запаса и имеющих разный наклон.
В двухпродуктовой экономике кривая предложения товара Y есть в то же время и кривая спроса субъекта А на благо X. Это следует из того, что она представляет множество оптимальных для субъекта А наборов благ X и Y при снижении цены X относительно цены Y.
Экономически кривая предложения из запаса показывает количество второго товара, до которого готов довести свой запас потребитель при различных соотношениях цен товаров.
Получим выражение кривой предложения из запаса, учитывая, что для неё, во-первых, выполняется условие оптимального потребительского выбора:
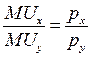 , (5.2)
, (5.2)
и, во-вторых, она соединяет бюджетные линии, проходящие через некоторую точку:
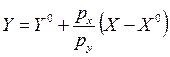 , (5.3)
, (5.3)
Выразив соотношение цен товаров из (5.3), 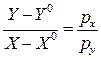 , и подставив в (5.2), получим:
, и подставив в (5.2), получим:
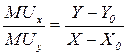 . (5.4)
. (5.4)
| Пример вывода выражения кривой предложения |
Например, для степенной функции полезности вида  имеем следующее выражение кривой предложения:
имеем следующее выражение кривой предложения:
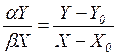 ,
,
откуда
 ,
,
следовательно
 . (5.5)
. (5.5)
Это уравнение определяет гиперболу, вертикальная асимптота (нуль знаменателя) которой имеет координату  , а горизонтальная асимптота (по правилу Лопиталя или как отношение коэффициентов при старших степенях дробно-рациональной функции) – координату
, а горизонтальная асимптота (по правилу Лопиталя или как отношение коэффициентов при старших степенях дробно-рациональной функции) – координату  . При этом предполагается, что
. При этом предполагается, что 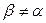 , иначе товары равноценны для потребителя и обмена не происходит. Таким образом, для монотонной кривой безразличия, характерной для степенной функции полезности, кривая предложения из запаса также монотонно убывает. Поэтому участок SAOCA правее точки А на рис. 5.2 (а) или левее точки В недопустим, так как это означает «обратный» эффект замены.
, иначе товары равноценны для потребителя и обмена не происходит. Таким образом, для монотонной кривой безразличия, характерной для степенной функции полезности, кривая предложения из запаса также монотонно убывает. Поэтому участок SAOCA правее точки А на рис. 5.2 (а) или левее точки В недопустим, так как это означает «обратный» эффект замены.
Кривая предложения касается кривой безразличия, которой принадлежит точка, характеризующая начальный набор товаров X и Y, в этой точке. Причем выше этой точки (товар Y дешевеет относительно товара X) кривая предложения имеет болеекрутой наклон, чем кривая безразличия, то есть потребитель готов принимать товар Y. Ниже точки начального набор товаров (товар Y дорожает относительно товара X) кривая предложения имеетменеекрутой наклон, то есть потребитель готов отдавать товар Y в обмен на товар X.
Дата добавления: 2020-10-25; просмотров: 661;











