Задача потребительского выбора

Геометрическое место точек (множество точек) пространства благ, для которых сумма затрат потребителя на их приобретение неизменна и равна доходу, называется бюджетной линией:

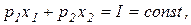(4.16)

где I (Income) - доход потребителя. Условие (4.16) выражает равенство доходов и расходов.

Изображенная на рис. 4.7 бюджетная линия аналогична рассмотренной выше линии ограниченного времени.

Экономический смысл бюджетной линии состоит в том, что она показывает количество второго товара, которое, истратив весь доход, может приобрести потребитель при различных количествах первого товара.

Рис. 4.7. Бюджетная линия

Пример 4.4.1. Для потребителя, получающего ежемесячный доход 300 руб. и 500 руб., построены бюджетные линии на рис. 4.7. По рис. видно, что, покупая 2 кг мяса, потребитель может приобрести 7 литров молока в месяц при доходе 300 руб. и 12 литров – при доходе 500 руб.

Потребитель при составлении набора благ решает следующую задачу: определить количество потребляемых благ 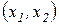, при которых максимизируется совокупная полезность

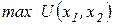
при выполнении бюджетного ограничения

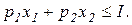
Графически задача выбора потребителя может быть решена путем построения семейства кривых безразличия и бюджетной линии (рис. 4.8):

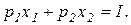
Затем из всех кривых безразличия выбирается та, которая касается бюджетной линии (то есть имеет одну общую точку с ней). Соответствующая этой кривой безразличия полезность U будет максимально возможной полезностью при данном доходе I, а сочетание 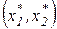- искомым набором благ.

Предпосылкой существования и единственности решения является выпуклость кривой безразличия, вытекающая из закона убывающей предельной полезности. На кривой безразличия этот закон выражается следующим образом: поскольку при единичном уменьшении потребления второго блага 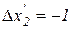объем первого блага растет на 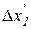, а при снижении второго блага на 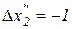первое благо потребляется на 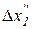больше, причем если

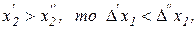
это означает что при большем исходном объеме заменяемого блага для его адекватной замены требуется меньшее количество блага-заменителя, и наоборот. Иными словами, предельная полезность блага 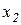ниже при большем объеме его потребления, чем при меньшем. Значит закон убывания предельной полезности соответствует убыванию предельной нормы замены (уменьшению угла наклона кривой безразличия к осям 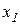или ).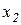

В точке А на рис. 4.8 с координатами 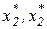угловые коэффициенты бюджетной линии и касательной к кривой безразличия (предельной нормы замены) равны:

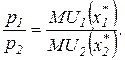(4.17)

то есть при оптимальной комбинации благ цена одного должна превосходить цену другого блага во столько же раз, во сколько раз первое благо полезнее второго.

Рис. 4.8. Решение задачи выбора

Пример 4.4.2. Потребитель, рассмотренный в примере 4.2.1, покупает молоко по цене 10 руб. за литр, а зубную пасту по цене 15 руб. за тюбик. Какой товарный набор наиболее выгоден для потребителя, если он может потратить на покупку этих товаров не более 120 руб. в месяц?

Запишем бюджетное ограничение: 10х₁+15х₂=120. Подставим выражения предельных полезностей, найденные в примере 4.2.1

, ,

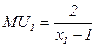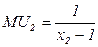а также цены товаров р₁=10, р₂=15 в условие оптимального выбора (4.17):

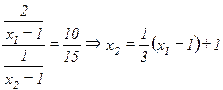. (4.18)

Подставим это выражение для х₂ в бюджетное ограничение: 10х₁+15[(х₁-1)/3+1]=120; откуда выразим оптимальный объем потребления первого товара: х^*₁=7,3 литра. Оптимальный объем потребления второго товара найдем по формуле (4.18): х^*₂=(х₁-1)/3+1=(7,3-1)/3+1=3,1 тюбика.

Таким образом, потребитель, приобретая 7,3 литра молока и 3,1 тюбика пасты в месяц при доходе в 120 руб. достигает максимального удовлетворения. Его уровень удовлетворенности при этом найдем, подставив оптимальные объемы потребления товаров в функцию полезности (пример 4.2.1):

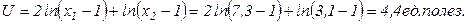
Пример 4.4.3. Предположим, что цены товаров в примере 4.4.2 возросли: молока на 2 руб., зубной пасты на 4 руб. Вследствие этого реальный доход, то есть покупательная способность потребителя, понизилась. Какую компенсацию должен получить потребитель, чтобы он мог приобрести товары в прежних количествах?

Если бы потребитель приобретал 1 литр молока и 1 тюбик пасты, то компенсация должна быть равна повышению цен: D р₁+Dр₂=2+4=6 руб. Но поскольку товарный набор потребителя х^*₁, х^*₂, то компенсация вычисляется по формуле:

DI=D р₁ х^*₁+Dр₂ х^*₂. (4.19)

Таким образом, чтобы сохранить прежний уровень удовлетворенности, потребитель должен получить 2*7,3+4*3,1=27 руб.; при таком приросте дохода он может приобрести прежний товарный набор по возросшим ценам.